Multidimensionale Skalierungen (MDS) in Excel

Dieses Tutorium wird Ihnen helfen, eine Multidimensional Scaling (MDS)-Analyse in Excel mithilfe der Software XLSTAT einzurichten und zu interpretieren.
Sie sind nicht sicher, ob dies das richtige Tool für die multivariate Datenanalyse ist, das Sie benötigen? Weitere Hinweise finden Sie hier.

Multidimensional Scaling

Die multidimensionale Skalierung (MDS) ist eine in den Bereichen Marketing und Psychometrie weit verbreitete Methode, insbesondere in den englischsprachigen Ländern. Das Prinzip der Methode besteht darin, eine Karte der Individuen auf Basis einer Proximitätsmatrix (Ähnlichkeiten oder Unähnlichkeiten) der Individuen zu konstruieren. Im Idealfall, in dem man über eine Abstandsmatrix zwischen den Punkten einer Ebene verfügt (beispielsweise die Abstände zwischen Städten in einer Region) rekonstruiert die MDS die Karte der Punkte, bis auf eine Rotation der Symmetrie genau. Um eine optimale Konfiguration zu berechnen, minimiert die Methode MDS ein Kriterium, das auch Stress genannt wird. Je näher dieses bei Null liegt, desto besser ist die Darstellung.

Datensatz für Multidimensional Scaling

Die Daten stammen aus einer Umfrage von 10 Verbrauchern, die gebeten wurden 5 Schokoladenriegel, von dem nur ein einziger auf dem Markt ist (Produkt P1), zu bewerten (Noten von 1 bis 5).

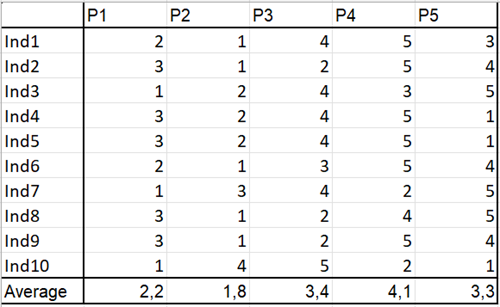
Ziel dieser Multidimensional Scaling-Analyse

Unser Ziel ist es zu zeigen, wie sich die Produkte auf einer Karte positionieren, basierend auf der Meinung der Tester.

Einrichten einer Multidimensional Scaling-Analyse

Erstellen einer Nähe-Matrix
Eine Nähe-Matrix ist erforderlich, um eine Multidimensional Scaling-Analyse durchzuführen. Hier haben wir jedoch eine Tabelle mit Individuen x Produkten. Daher müssen wir zuerst die Unähnlichkeiten zwischen den Produkten berechnen, was mit dem Tool für Ähnlichkeits-/Unähnlichkeitsmatrizen von XLSTAT durchgeführt werden kann.
Sobald XLSTAT aktiviert ist, klicken Sie auf das Menü "Daten beschreiben" und wählen Sie "Ähnlichkeits-/Unähnlichkeitsmatrizen" aus (siehe unten).

Die Dialogbox erscheint. Sie können dann die Daten auf dem Excel-Blatt auswählen und die entsprechenden Optionen wie unten gezeigt auswählen. Wir entscheiden uns dafür, die Nähe-Matrix direkt unter den Originaldaten auf dem gleichen Blatt anzuzeigen.

Die Nähe-Matrix wird standardmäßig generiert und muss nicht als spezifischer Ausgabepunkt angegeben werden. Die Berechnungen beginnen, sobald Sie auf OK geklickt haben.
Sie erhalten dann die Matrix der euklidischen Abstände zwischen den Produkten, die die Grundlage für die Multidimensional Scaling-Analyse darstellen wird.

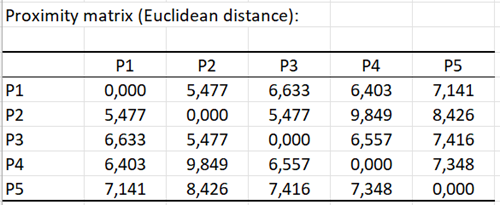
Einrichten des Dialogfelds für die Multidimensionale Skalierung
Klicken Sie anschließend auf das Menü "Daten analysieren" und wählen Sie den Befehl "Multidimensionale Skalierung" aus (siehe unten).

Die Dialogbox für die Multidimensionale Skalierung wird angezeigt.
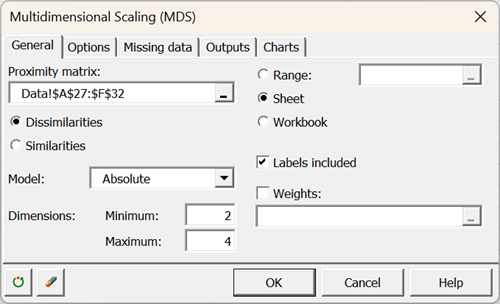
Sie können dann die Distanzmatrix auf dem Excel-Blatt auswählen und die entsprechenden Optionen wie unten gezeigt auswählen.
Das absolute Modell wurde ausgewählt; dieses Modell sorgt dafür, dass die Abstände in der endgültigen Darstellung so nah wie möglich an den ursprünglichen euklidischen Abständen liegen.
Andere Optionen können ähnliche Ergebnisse liefern, aber es könnte ein Skaleneffekt eingeführt werden, den wir hier entfernen möchten.
Wir bitten darum, dass die Analyse von 4 auf 2 Dimensionen durchgeführt wird, um die mit der Dimensionsreduzierung verbundene Verzerrung zu bewerten.

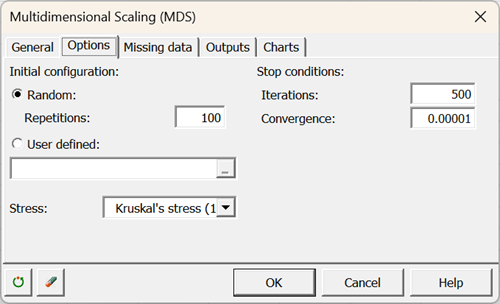
Hinweis: Wenn Sie dem Algorithmus keinen Startpunkt im Register "Optionen" geben, werden die Startpunkte zufällig ausgewählt. Daher ist es wahrscheinlich, dass die Ergebnisse, die Sie erhalten, leicht von denen auf dieser Seite abweichen. Dies sollte jedoch die Interpretation nicht beeinträchtigen. Um sicherzustellen, dass der Algorithmus ein echtes Optimum (in Bezug auf Stress) findet, können Sie die Anzahl der Wiederholungen, die maximale Anzahl der Iterationen und die Genauigkeit erhöhen.

Die Berechnungen beginnen, sobald Sie auf "OK" geklickt haben. Nachdem Sie zugestimmt haben, die Karte auf den ersten beiden Dimensionen zu plotten, indem Sie auf "Fertig" klicken, werden die Ergebnisse auf dem Tab "Multidimensional Scaling" des Excel-Arbeitsblatts angezeigt.

Interpretieren der Ergebnisse von Multidimensional Scaling

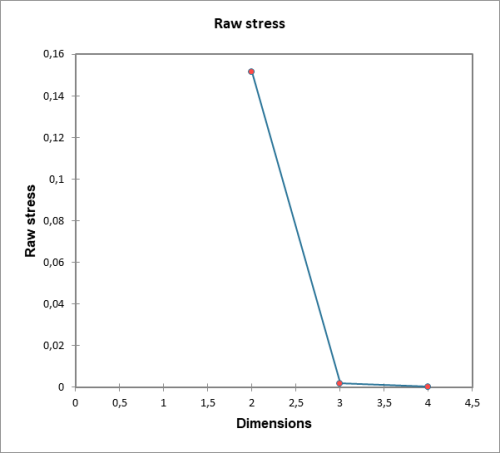
Die erste Tabelle zeigt die Entwicklung des Stresswerts mit zunehmender Anzahl der Dimensionen. Wir bemerken einen deutlichen Bruch zwischen den 2-dimensionalen und 3-dimensionalen Darstellungen und eine Stabilität zwischen 3 und 4 (es ist mathematisch normal, dass eine 4D-Darstellung für 5 Punkte perfekt ist).

Eine Karte wird auf der Ebene Dim1 x Dim2 für die 2-dimensionale Konfiguration erstellt.

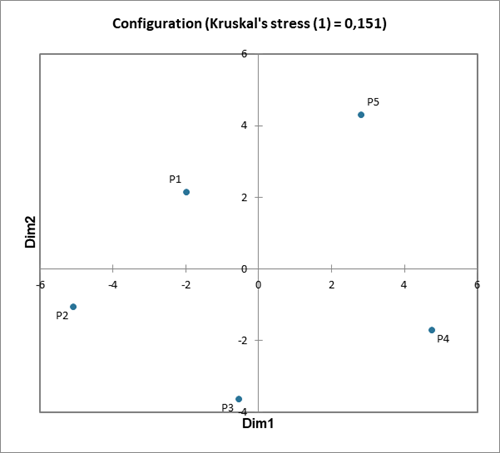
Es ist auch möglich, Karten für einige andere Achsenpaare für die 3D- oder 4D-Konfigurationen zu erstellen. Es wird jedoch nicht empfohlen, die Karte für eine Konfiguration, die für mehr Dimensionen erstellt wurde, in zwei Dimensionen anzuzeigen, da es zu einem Projektionseffekt kommen kann, der jede Interpretation falsch macht. Die 2D-Karte sollte nur für die 2-dimensionale Konfiguration verwendet werden. Um die 4D-Konfiguration auf einer 2D-Karte anzuzeigen, sollte zunächst eine PCA auf den Koordinaten durchgeführt werden.
Um eine noch bessere Qualität der Darstellung zu erhalten, verwenden wir XLSTAT-3DPlot, um die Daten in drei Dimensionen zu plotten. Dazu müssen wir die Daten auswählen:

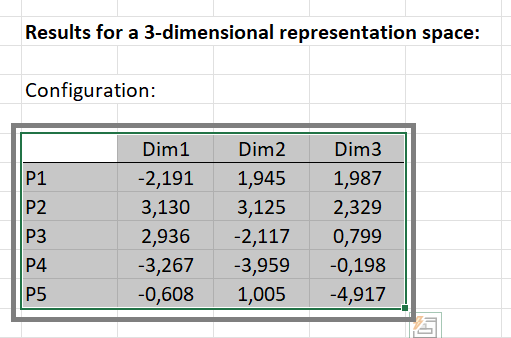
Und auf die Schaltfläche "XLSTAT-3DPlot" im Menü "Daten visualisieren" klicken:

Das Ergebnis, das wir erhalten, sieht wie folgt aus:

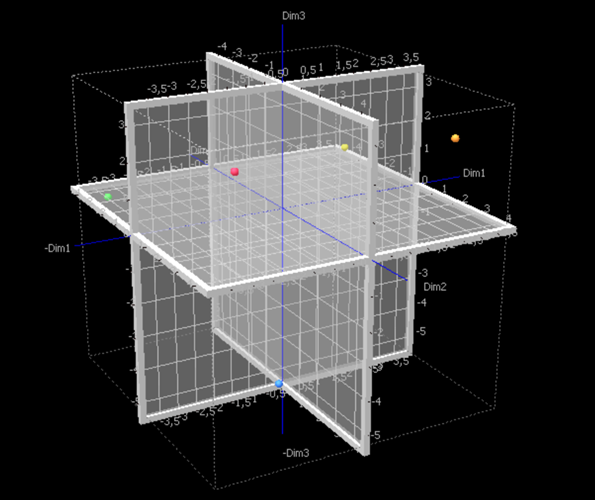
Es ist erkennbar, dass die Tester die Produkte kollektiv gut voneinander unterschieden haben. Wir wissen, dass das Produkt P2 mehr Schokolade enthält als P4, das am wenigsten Schokolade enthält: Auf dem 3D-Diagramm sehen wir, dass sie diametral gegensätzlich sind. Bei Betrachtung des Ausgangsdatensatzes können wir feststellen, dass die Tester das Produkt P2 signifikant bevorzugt haben. Wir können auch sehen, dass, obwohl sie ähnliche Durchschnittsbewertungen haben, die Produkte P3 und P5 nicht nah im Darstellungsraum liegen: Die Meinungen der Tester sind manchmal gegensätzlich. Das lässt sich darauf zurückführen, dass dem Produkt P3 einige Erdnüsse hinzugefügt wurden, was von einigen Testern geschätzt wird und von anderen nicht.

Schlussfolgerung über Multidimensional Scaling

Als Fazit ermöglicht die Multidimensionale Skalierungsmethode, die Produkte zu kartieren, die von den Testern bewertet wurden. Sie erlaubt eine viel reichhaltigere Interpretation als einfache Statistiken.
Hinweis: Es gibt keine strenge statistische Methode, um die Qualität und Zuverlässigkeit einer durch eine Multidimensionale Skalierung durchgeführten Darstellung zu bewerten. Durch die Betrachtung des Shepard-Diagramms kann jedoch eine allgemeine Vorstellung von der Qualität der Darstellung gewonnen werden. Das Shepard-Diagramm entspricht einem Streudiagramm, bei dem die Abszissen die beobachteten Unähnlichkeiten und die Ordinaten die Distanz in der von der Multidimensionalen Skalierung generierten Konfiguration sind. Die Unterschiede werden ebenfalls angezeigt. Je weiter die Punkte verteilt sind, desto weniger zuverlässig ist die Multidimensionale Skalierungskarte. Wenn die Rangfolge der Abszisse auf den Ordinaten respektiert wird, dann ist das Diagramm zuverlässig. Wenn die Punkte auf derselben Linie liegen, ist die Qualität perfekt.

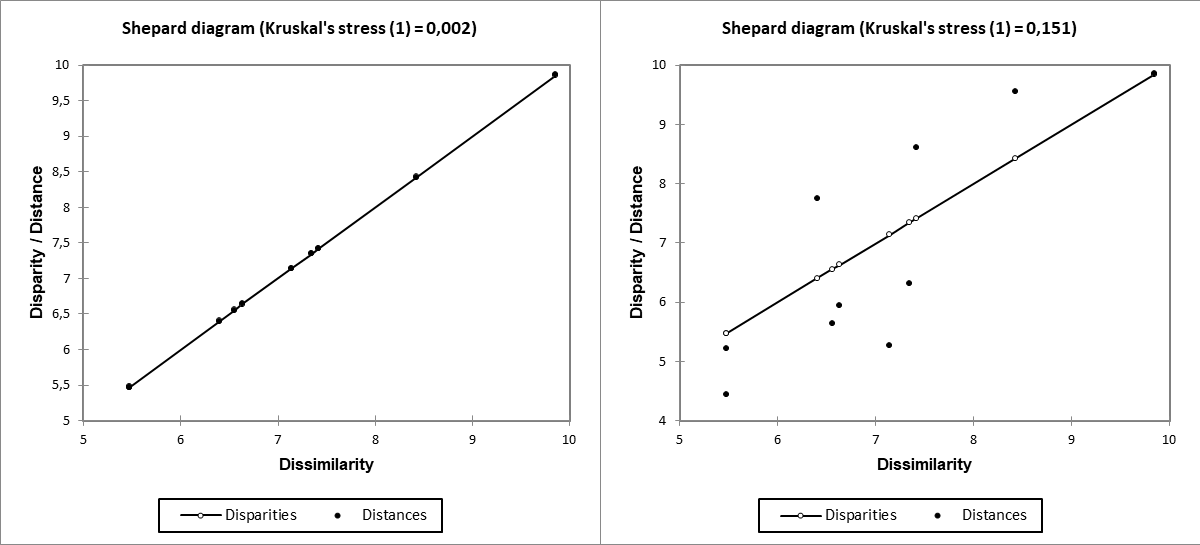
Die Grafik auf der linken Seite entspricht für die in diesem Beispiel verwendeten Daten der Darstellung in einem 4D-Raum. Die Grafik auf der rechten Seite entspricht der Darstellung im 2D-Raum. Wir bemerken einen deutlichen Unterschied in der Ausbreitung der Punkte zwischen den beiden Diagrammen.
Hinweis: Für ein absolutes Modell sind die Diskrepanzen gleich den Unähnlichkeiten, weshalb sie mit der Linie für den 2D-Raum verwechselt werden und hinter den Distanzen auf dem 4D-Sheppard-Diagramm verborgen sind.
Das folgende Video behandelt die Multidimensionale Skalierung mit einer Veranschaulichung in XLSTAT.