Clusters de k-means: tutorial en Excel

Este tutorial le ayudará a configurar e interpretar un cluster de k-means en Excel utilizando el software XLSTAT.
¿No está seguro de que esta sea la herramienta de clustering que necesita? Consulta esta guía.

Conjunto de datos para cluster de k-means

Nuestros datos provienen de la Oficina del Censo de los EE.UU. y describen los cambios en la población de 51 estados entre 2000 y 2001. El conjunto de datos inicial se ha transformado en tasas por cada 1000 habitantes, utilizando los datos de 2001 como enfoque para el análisis.

Objetivo de este tutorial

Nuestro objetivo es crear clústeres homogéneos de estados basados en los datos demográficos disponibles. Este conjunto de datos también se utiliza en el tutorial de Análisis de Componentes Principales (ACP) y en el tutorial de Clasificación Ascendente Jerárquica (CAJ).

Nota: Si intenta repetir el mismo análisis descrito a continuación con los mismos datos, como el método k-means comienza con clústeres seleccionados al azar, es muy probable que obtenga resultados diferentes de los que se enumeran aquí, a menos que fije la semilla de los números aleatorios al mismo valor que se utilizó aquí (4414218). Para fijar la semilla, vaya a las Opciones de XLSTAT, pestaña Avanzado, y luego marque la opción Fijar la semilla.

Configuración de un cluster de k-means en XLSTAT

• Una vez que XLSTAT esté abierto, haga clic en Analizar datos / Clustering k-means.

• Aparece el cuadro de diálogo de clustering k-means.

• Seleccione los datos en la hoja de Excel. En este ejemplo, los datos comienzan en la primera fila, por lo que es más rápido y fácil utilizar el modo de selección de columnas. Esto explica por qué las letras correspondientes a las columnas se muestran en las casillas de selección.

• La variable POBLACIÓN TOTAL no fue seleccionada, ya que nos interesan principalmente las dinámicas demográficas. La última columna (> 65 POB. EST.) no fue seleccionada porque está completamente correlacionada con la columna anterior.

• Dado que el nombre de cada variable está presente en la parte superior de la tabla, debemos marcar la casilla de etiquetas de variables.

• El criterio seleccionado es el Determinante(W), ya que le permite eliminar los efectos de escala de las variables.

• Se elige la distancia euclidiana como el índice de disimilitud porque es la más clásica para utilizar en el clustering k-means.

• Establecemos el número de clústeres a crear en 4.

• Finalmente, se seleccionan las etiquetas de fila (columna ESTADO) porque se especifica el nombre del estado para cada observación.

• En la pestaña Opciones, aumentamos el número de repeticiones a 10 para mejorar la calidad y la estabilidad de los resultados.

• Finalmente, en la pestaña Salidas, podemos elegir mostrar una o varias tablas de salida.

Interpreting a k-means clustering

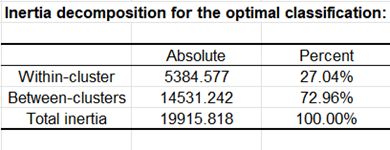
Después de las estadísticas descriptivas básicas de las variables seleccionadas y el resumen de la optimización, el primer resultado mostrado es la tabla de descomposición de la inercia.

Se muestra la tabla de descomposición de la inercia para la mejor solución entre las repeticiones. (Nota: Inercia total = Inercia entre clases + Inercia dentro de la clase).

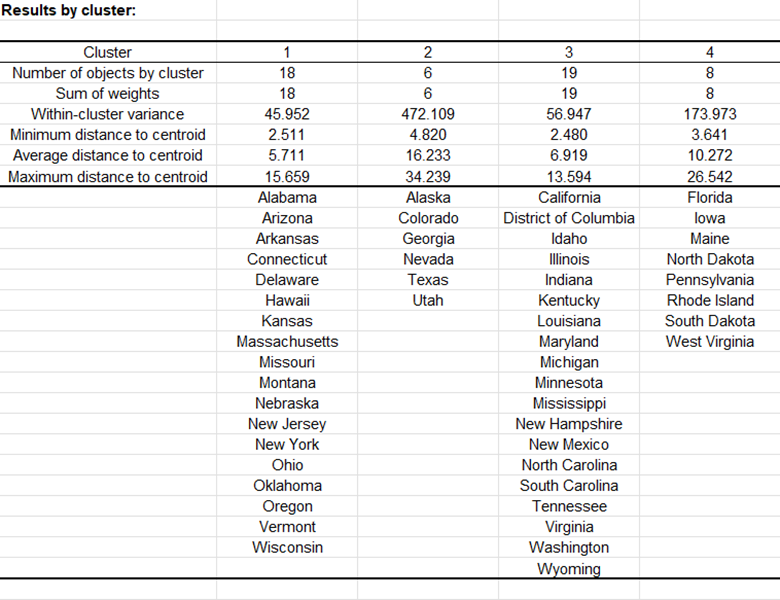
Después de una serie de tablas que incluyen los centroides de las clases, la distancia entre los centroides de las clases, los objetos centrales (aquí, el estado que está más cercano al centroide de la clase), una tabla muestra los estados que han sido clasificados en cada clúster.

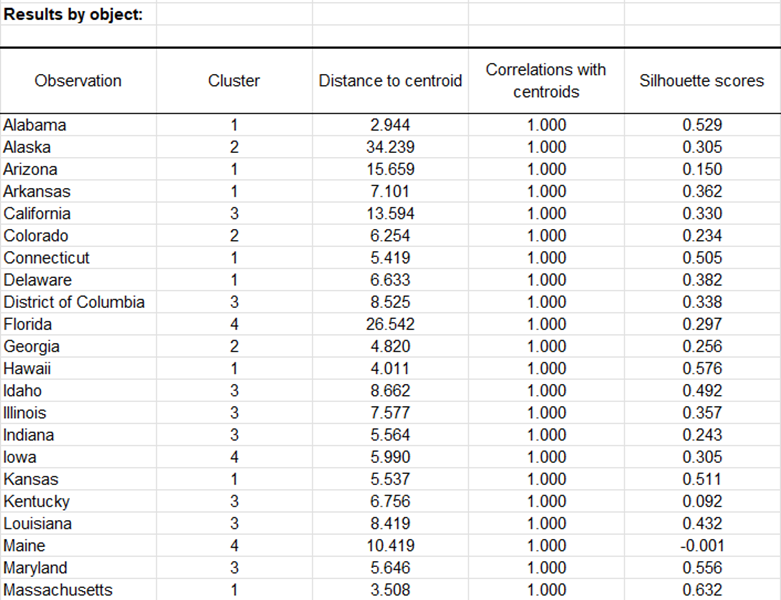
Luego se muestra una tabla con la identificación del grupo para cada estado. A continuación se muestra un ejemplo. Las identificaciones de los clústeres pueden fusionarse con la tabla inicial para realizar análisis adicionales (por ejemplo, análisis discriminante).
Las opciones Correlaciones con centroides y Puntajes de Silueta están activadas, y luego se muestran las columnas asociadas en la misma tabla:

Un gráfico que representa los puntajes de silueta le permite estudiar visualmente la calidad del agrupamiento. Si el puntaje está cerca de 1, la observación se encuentra bien en su clase. Por el contrario, si el puntaje está cerca de -1, la observación se asigna a la clase incorrecta.

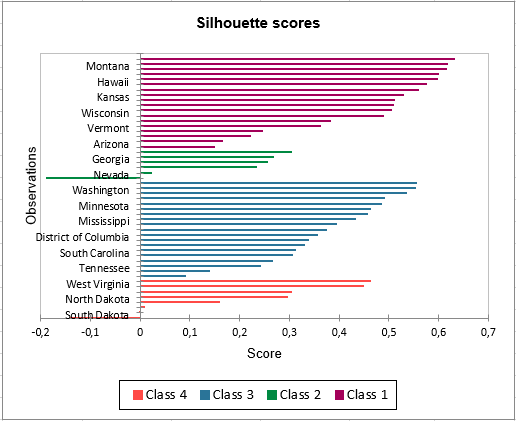
Los puntajes medios de silueta por clase le permiten comparar clases y determinar cuál es la más uniforme según este puntaje.

La Clase 1 tiene los puntajes de silueta más altos. Mientras tanto, la Clase 2 tiene un puntaje cercano a 0, lo que significa que 4 no es el mejor número de clases para estos datos. En el tutorial sobre Clasificación Jerárquica Aglomerativa (AHC), vemos que los Estados estarían mejor agrupados en tres grupos.

Este video le muestra cómo agrupar muestras con el clustering k-means.