Histogramas y ajuste de distribuciones Excel

El objetivo de este tutorial es el de general un histograma y una prueba de bondad de ajuste para saber si una muestra sigue una distribución binomial negativa por medio de la herramienta ajuste de una distribución de XLSTAT en Excel. Esta distribución suele usarse para representar el fenómeno de agregación/dispersión de bacterias en ambientes acuáticos.

Datos para crear un histograma y ajustar una distribución

Arriba se encuentra una liga en donde

Los datos corresponden a un experimento donde se cultivaron 200 muestras de agua extraídas de un río el cual se encontraba en medio de nutrientes para determinar la presencia o ausencia de contaminación bacteriana con Escherichia coli. Se ha contado el número de colonias después de 72 horas de incubación. Dentro del archivo de Excel, en la columna Bact-Data se encuentran los recuentos de las 200 muestras.

Configuración del cuadro de diálogo para crear un histograma

Ya abierto XLSTAT, se selecciona el comando XLSTAT/Visualización de datos/Histogramas (ver imagen).

Una vez abierta la caja de diálogo, seleccionar los datos de la hoja de Excel que se llama Data.

En la pestaña general, se selecciona la columna B en el recuadro donde dice Datos. En este caso se activa la opción de Tipo de datos: Discreto porque el recuento de las colonias son datos discretos. También se activa el recuadro de Etiquetas de las variables porque la primera fila de la selección de los datos incluye el nombre de la muestra. Se selecciona el botón de OK para que empiece el cálculo computacional. Los resultados se mostraran en una nueva hoja.

Interpretación de un histograma

El histograma se muestra en la hoja Histograma debajo de la tabla Estadísticos descriptivos. Y debajo del histograma se encuentra una tabla que muestra los Estadísticos descriptivos para los intervalos.

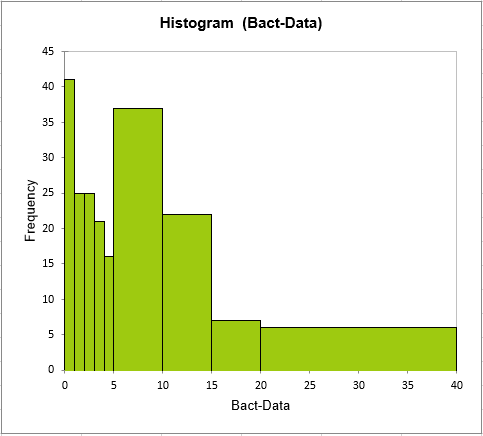
En el histograma se puede observar que el valor más frecuente es 0, el cual representa más del 20% de los datos. Esto significa que en más de una muestra cada cinco no se encontró bacterias. Así mismo, también se observa que la frecuencia decrece rápidamente. Por otro lado, en una muestra se contabilizaron más de 36 colonias.

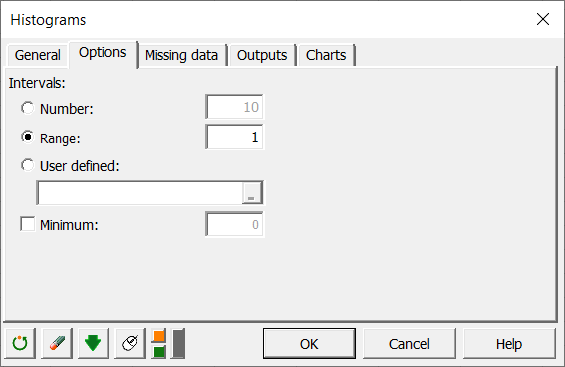
Crear un histograma especificando los límites de los intervalos.

Como se quiere probar el ajuste entre la función de distribución binomial y la muestra (la prueba de bondad de ajuste Chi-Cuadrado requiere que haya al menos 5 datos por clase), y debido a la precisión incierta de los recuentos de bacterias, parece necesario agrupar los conteo es clases más grandes. Por esa razón, se crea una lista de límites que parecen coherentes con el problema que se tiene: 0,1,2,3,4,5,10,15,20,40. Para verificar que las frecuencias de las nuevas clases son superiores a 5 y que disminuyen regularmente, se crea un nuevo histograma. Con la diferencia que esta vez se especifican los límites de los intervalos en la pestaña Opciones. 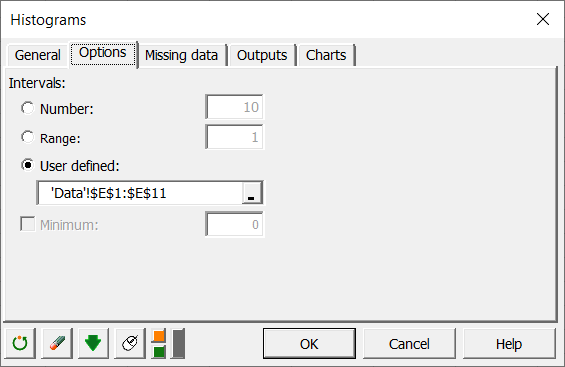Los cálculos computaciones empiezan una vez que se selecciona el botón de OK. Posteriormente aparece un nuevo histograma (en la hoja “Histograma1”). Como se está satisfecho con este resultado, se puede usar la herramienta de ajuste de una distribución para probar si la muestra sigue una distribución binomial negativa.

Configuración de la caja de diálogo para ajustar una distribución

Se selecciona el comando de XLSTAT/Modelación de datos/Ajuste de una distribución (ver imagen).

A continuación aparece el cuadro de diálogo de la herramienta de ajuste de una distribución. Se selecciona los datos en la hoja de Excel llamada Datos.

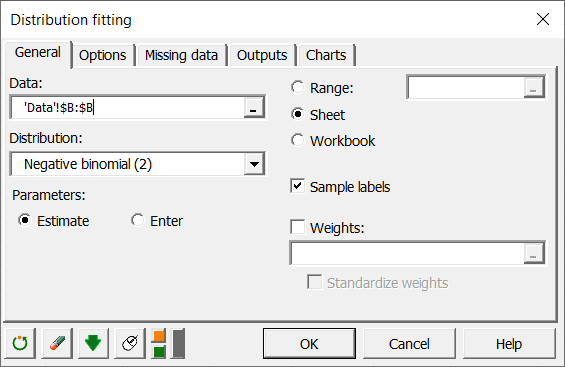
En la pestaña general, se selecciona la columna B en el recuadro de Datos. También se deja que XLSTAT estime los parámetros de la función de distribución binomial negativa. XLSTAT ofrece dos diferentes formulaciones de la distribución binomial negativa. Usaremos la segunda formulación porque es la que se ajusta a nuestro caso. En la pestaña de Opciones se selecciona la Prueba de Chi-Cuadrado, la cual es la necesaria para probar nuestra suposición. Así mismo se usan los límites de los intervalos que se definieron anteriormente. Se seleccionan las siguientes opciones en la pestaña de Gráficos.

Interpretación de los resultados del análisis de un ajuste de distribución

El primer resultado de interés para el análisis es el de los valores k y p de los parámetros de la distribución binomial negativa (ajustados por medio del método de máxima verosimilitud), los estimadores muestrales, la media teórica, varianza, sesgo y kurtosis. Mientras más cercanos estén estos valores muestrales (obtenidos de los datos) con respecto a los teóricos, el ajuste es mejor. En este caso, el ajuste es excelente. Nota: La media teórica está dada por kp y la varianza por kp(p+1).

La prueba de bondad de ajuste de Chi-Cuadrado permite evaluar si la distancia Chi-Cuadrada entre la distribución teórica y empírica está por encima de un valor crítico o no. Una comparación visual entre las frecuencias teóricas y observadas se encuentran en la siguiente figura. 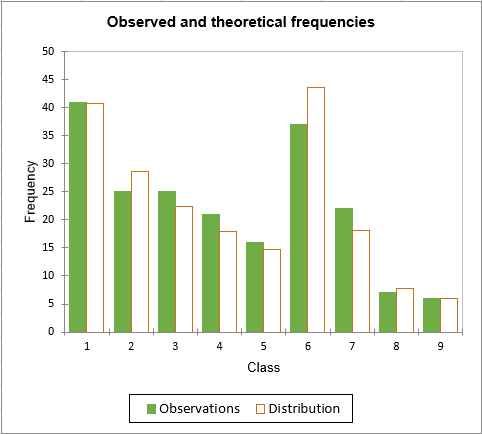Pareciera que hay una pequeña diferencia para las clases 2,6 y 7. Sin embargo, el valor-p calculado para esta prueba (0.77) es significativamente más alto que el nivel de significancia que se ha escogido (0.05). Por lo tanto, la prueba Chi-Cuadrada confirma la hipótesis de que los datos provienen de una distribución binomial negativa. 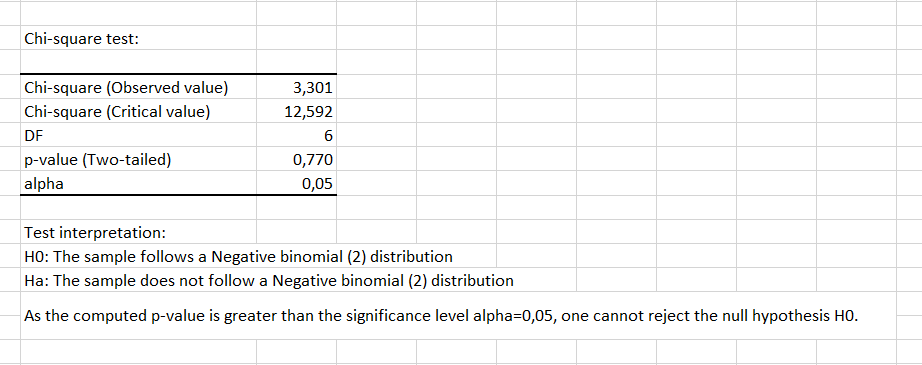Finalmente, se puede decir que la presencia de la bacteria de interés en el río en donde se tomó la muestra sigue una distribución binomial negativa con parámetros (k = 0.823, p=5.921), con una media de 4.8 y una varianza de 33.4.