Apprentissage d'une machine à vecteurs de support une classe dans Excel

Ce tutoriel vous aidera à mettre en place une méthode de Machine à Vecteurs de Support à une classe (SVM à une classe) dans Excel en utilisant le logiciel de statistiques XLSTAT.

Jeu de données pour entrainer une SVM à une classe

Le jeu de données utilisé dans ce tutoriel provient de la plateforme de data science, Kaggle et est accessible à cette adresse.

Le jeu de données « Banknotes » est constitué d'une liste de 200 billets de banque contrefaits ou non. Le jeu de données est composé de 7 variables dont une informe sur l’authenticité du billet de banque tandis que les 6 autres sont des variables quantitatives donnant les caractéristiques d’un billet.

Counterfeit : si le billet de banque est authentique on notera « 0 », dans le cas contraire où le billet est contrefait alors on notera « 1 ». Dans ce jeu de données, 100 billets sont authentiques et 100 billets sont contrefaits.

Length, Left, Right, Bottom, Top et Diagonal sont les variables quantitatives précisant les mesures et dimensions des billets de banque.

Un deuxième jeu de données constitué de 10 billets de banque est disponible pour prédire leur classe, c’est-à-dire s’ils sont contrefaits ou non.

Objectif de ce tutoriel

L'objectif de ce tutoriel est d'apprendre à détecter des anomalies avec une méthode de SVM à une classe sur le jeu de données « Banknotes » et voir les performances que nous obtenons en lançant une validation croisée 10-folds.

Mettre en place une méthode de SVM à une classe dans Excel avec XLSTAT

Pour mettre en place une méthode de SVM à une classe, cliquez sur Machine Learning / Machines à Vecteurs de Support à une classe comme indiqué ci-dessous : 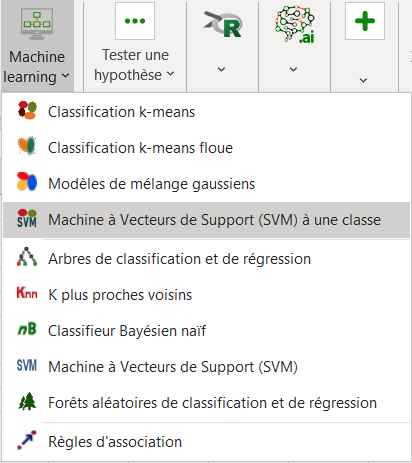Une fois que vous avez cliqué sur le bouton, la boîte de dialogue apparait. Sélectionnez les données dans la feuille Excel.

Il faut d’abord sélectionner des variables explicatives quantitatives en activant l’option comme indiqué ci-dessous. 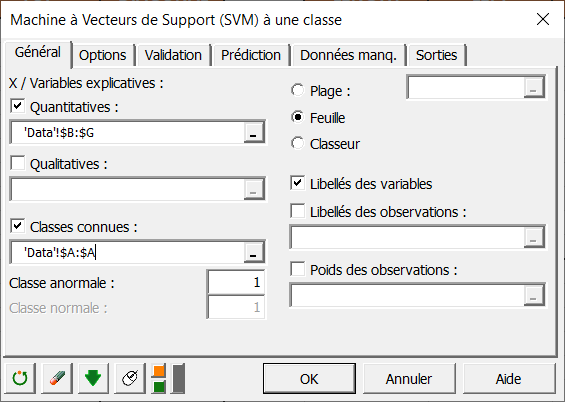Dans le champ Quantitatives, sélectionnez toutes les variables quantitatives : « Length », « Left », « Right », « Bottom », « Top » et « Diagonal ».

Pour sélectionner plusieurs colonnes, utilisez la touche Ctrl de votre clavier.

Le jeu de données comprend une variable indiquant par un « 1 » si le billet est contrefait et 0 si le billet ne l’est pas. Cette variable peut être utilisée pour calculer la performance de la machine à vecteurs de support à une classe. Pour cela, cochez Classes connues puis sélectionnez la variable binaire « Counterfeit ». Enfin, entrez le libellé indiquant les billets contrefaits, ici nous entrons « 1 » en tant que Classe anormale.

Comme le nom de chaque variable est présent au début du fichier, assurez-vous que la case Libellés des variables est cochée.

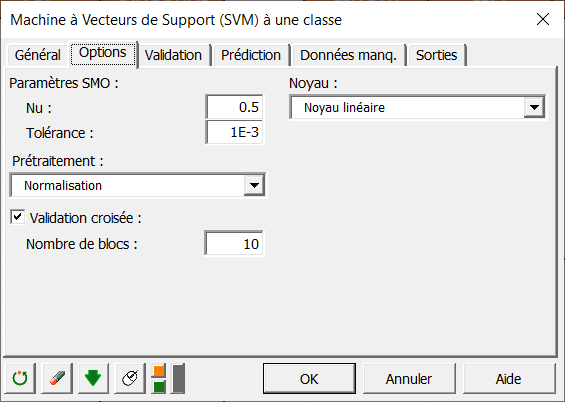
Dans l'onglet Options, vous pouvez régler les paramètres du classifieur. Pour les paramètres SMO, le champ Nu correspond à la variable de régularisation. Elle traduit le pourcentage d’observations anormales que vous souhaitez autoriser durant l'optimisation. Plus la valeur de Nu est proche de 1 et plus grand sera le pourcentage d’observations considérées anormales.

Le paramètre de tolérance indique le niveau de précision souhaité durant l'optimisation. Pour accélérer les calculs, vous pouvez augmenter la valeur de ce paramètre. Nous le laissons à sa valeur par défaut.

Pour le prétraitement, nous choisissons normalisation et nous utiliserons des noyaux linéaires comme indiqué ci-dessous.

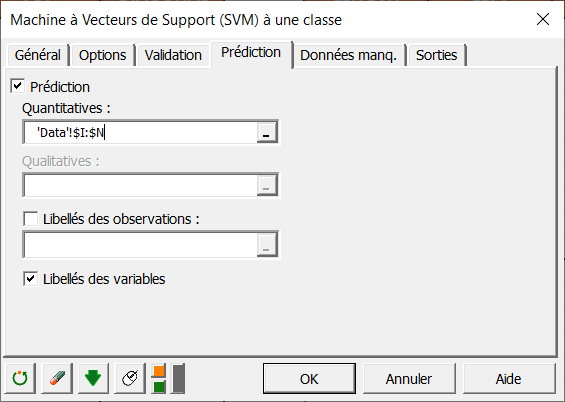
Enfin, pour valider notre modèle, nous pouvons lancer une validation croisée 10-folds. Comme on veut prédire la classe des 10 nouvelles observations, dont la classe est inconnue, on sélectionne dans l’onglet Prédictions les 6 variables quantitatives. Comme le nom de chaque variable est aussi présent au début du fichier, assurez-vous que la case Libellés des variables est cochée. Finalement dans l’onglet sorties, sélectionner les sorties comme indiqué ci-dessous : Les calculs démarrent lorsque vous cliquez sur OK. Les résultats sont ensuite affichés.

Interpréter les résultats d’une SVM à une classe et d’une validation croisée 10-folds

Le premier tableau donne les résultats de performance de la validation croisée. Pour chacun des 10 blocs, le taux d’erreur de classification, la F-mesure et la précision équilibrée (Balanced ACcuracy) sont affichés. En moyenne, le taux d’erreur de classification par validation croisée est de 29.1% pour un modèle utilisant les paramètres choisis précédemment. Ensuite, les performances de classification sur le jeu de données d’apprentissage sont données dans un tableau avec 10 indicateurs : 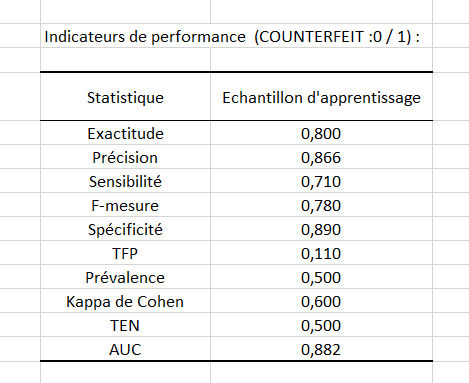Dans le cas d’une classification à une classe, la F-mesure est à préférer à la précision. Ici, la F-mesure est de 78% ce qui signifie que le modèle est assez efficace pour détecter des anomalies.

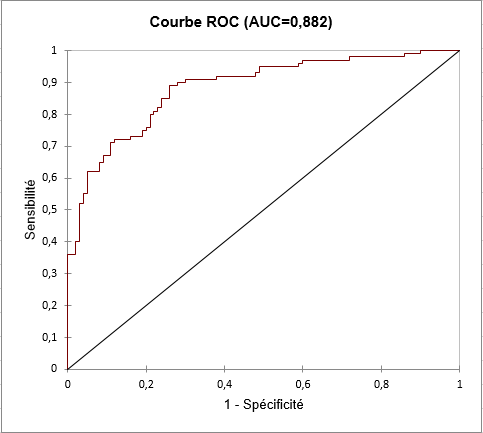
Nous pouvons nous aider de la courbe ROC pour évaluer notre modèle. La courbe ROC correspond à la représentation graphique du couple (1 – spécificité ; sensibilité) pour les différentes valeurs seuil.

Nous cherchons à avoir une courbe qui se rapproche du coin supérieur gauche, ce qui est le cas ici : Nous pouvons ensuite regarder les résultats associés à notre classifieur.

Le premier tableau donne un résumé des caractéristiques du classifieur obtenu. Vous pouvez voir sur la figure ci-dessous que la classe 1 a bien été marquée comme la classe anormale, que l’on peut aussi appeler classe négative. 200 observations ont été utilisées pour entrainer le classifieur, parmi celles-ci, 113 ont été identifiées comme vecteurs de support et un biais proche de zéro a été calculé. 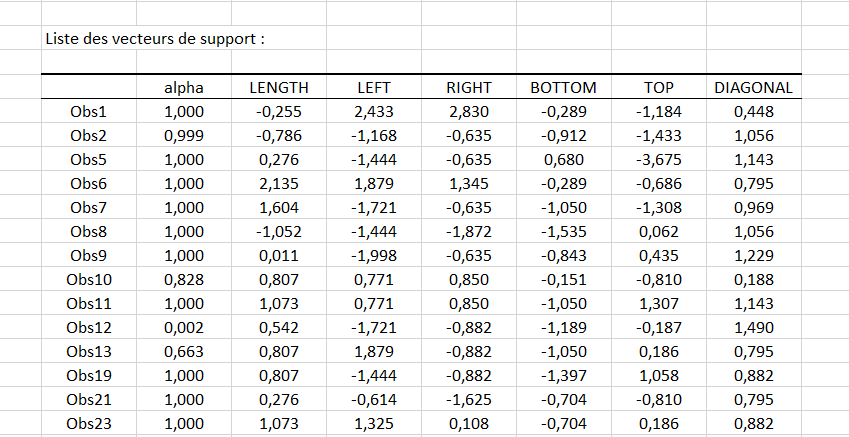Le second tableau montré ci-dessous, donne la liste complète des 113 vecteurs de support avec le coefficient alpha associé. Ce coefficient ainsi que le biais donné dans le tableau précédent suffisent à décrire complètement le classifieur optimisé. Enfin, nous trouvons les prédictions proposées par la méthode pour les 10 observations dont la classe est inconnue : la première colonne montre la classe prédite pour chaque observation, tandis que la deuxième colonne est le résultat de la fonction de décision. 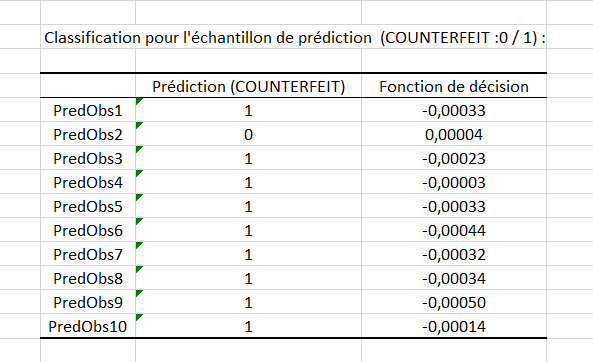Comme nous avons choisi « 1 » comme valeur pour la classe anormale, les observations prédites « 1 » par l’algorithme sont donc ici des anomalies.