Quel outil d’analyse de séries temporelles choisir ?

Ce guide décrit des outils d’analyse de séries temporelles ou séries chronologiques et vous aidera à choisir quelle méthode choisir en fonction de vos besoins.

Toutes les méthodes mentionnées ci-dessous se trouvent dans le menu Analyse de données temporelles du logiciel XLSTAT, à l’exception de la régression linéaire, qui se trouve dans le menu Modélisation des données.

Qu’est-ce qu’une série temporelle ?

Une série temporelle ou série chronologique est une séquence de points de données alignés dans un ordre temporel. Les données sont généralement également espacées. Les séries temporelles sont utilisées dans une grande variété de domaines. En économétrie et en finance, les séries temporelles comprennent le suivi dans le temps des taux de change, des cours des actions ainsi que de nombreuses autres variables. En météorologie, les mesures mensuelles de précipitations ou de températures effectuées sur plusieurs années sont des séries temporelles.

Première chose à faire : visualiser la série temporelle

Quel que soit l’objectif, il est recommandé de visualiser la série temporelle pour détecter de potentielles valeurs aberrantes ou découvrir visuellement les tendances, les comportements saisonniers ou d'autres motifs courants qui seront abordés plus en détail ci-dessous. La visualisation des séries temporelles est la première fonctionnalité qui apparaît sous le menu d'analyse de séries temporelles dans XLSTAT. Cette fonction offre la possibilité d'afficher plusieurs séries simultanément.

Vous trouverez ci-dessous un exemple de données mensuelles sur les passagers internationaux (en milliers) de l'aéroport de San Francisco de janvier 1949 à décembre 1960 [Box, G. E. P., Jenkins, G. M. and Reinsel, G. C. (1976) Time Series Analysis, Forecasting and Control. Third Edition. Holden-Day. Series G].

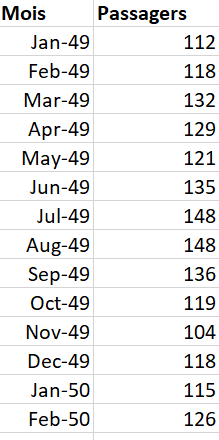
La série temporelle du nombre de passagers (en milliers) est affichée graphiquement ci-dessous :

Les étapes qui suivent dépendent de la question posée

Plusieurs questions peuvent être posées autour de données de séries temporelles :

• Après avoir supprimé le bruit, quelles sont les caractéristiques globales d'une série temporelle, en termes de tendance, de saisonnalité et de variance ?
• Comment étudier le lien entre des variables qui dépendent du temps ? Par exemple, pouvons-nous expliquer la consommation des ménages par leurs revenus en se basant sur des données historiques mensuelles?
• Comment prédire les valeurs futures d'une série temporelle ?
• Comment mesurer les cycles dans une série temporelle ?

Chacune de ces questions sera abordée dans une section différente par la suite.

Etudier les tendances, la variance et la saisonnalité

Quelles sont les principales caractéristiques de la série temporelle affichée dans le graphique précédent ?

a. Tendance et moyenne d’une série temporelle

Il est d’abord intéressant de noter la tendance globale d’une série temporelle, en faisant abstraction des variations qui l’entourent. L'idée est d'étudier l’évolution de la moyenne de la série temporelle au cours du temps.

Il semble évident que la série temporelle sur les passagers présente une tendance croissante. Le nombre de passagers a augmenté de 1949 à 1960.

La fonctionnalité de lissage configurée avec l’option moyenne mobile permet de découvrir la forme de la tendance globale tout en excluant le bruit.

Le test non-paramétrique de tendance de Mann-Kendall peut être utilisé pour étudier la significativité d’une tendance globale croissante ou décroissante. La pente de Sen mesure la force et la direction de la tendance. Le test de Mann-Kendall est significatif sur la série des passagers.

Les tests d'homogénéité, y compris ceux de Pettitt, SNHT, Buishand et Von Neumann, aident à tester la présence d’un changement brusque de la moyenne de la série temporelle à une date donnée. Ces tests révèlent tous le moment précis où le changement se produit, à l'exception du test de Von Neumann.

b. Variance d’une série temporelle

La variance d’une série temporelle peut évoluer au cours du temps. C'est le cas de la série des Passagers, qui montre une variance croissante au fil des années. Cela se traduit par la largeur croissante de la série chronologique dans le temps.

c. Saisonnalité dans une série temporelle

Enfin, la série temporelle affiche un motif qui semble se répéter d'année en année. Par exemple, le nombre de passagers atteint systématiquement son maximum pendant les mois d'été. On parle de saisonnalité.

d. Décomposer une série temporelle en ses composantes tendancielle et saisonnière

La fonctionnalité de transformation de séries temporelles permet de diviser une série temporelle en plusieurs composantes, notamment la tendance, le bruit saisonnier et le bruit aléatoire restant. Deux modèles sont possibles :

• Modèle additif : la série temporelle originale peut être reconstituée en additionnant les trois composantes.
• Modèle multiplicatif : la série temporelle originale peut être reconstruite en multipliant les trois composantes. Cette option est appropriée lorsque la variance de la série chronologique change au cours du temps.

​​​​Le graphique ci-dessous affiche le résultat d’une décomposition multiplicative de la série temporelle des passagers :

Comment étudier les liens entre variables qui dépendent du temps ?

a. Utiliser les modèles de régression classiques sur des séries temporelles : l'importance de la stationnarité

Les modèles de régression permettent d’expliquer une variable dépendante par une série de variables indépendantes. Par exemple, on peut chercher à identifier quelles variables, notamment les cours boursiers ou certaines actions marketing, expliquent au mieux le chiffre d’affaires d’une entreprise. Lorsque les données utilisées dans la régression dépendent du temps, comme par exemple le chiffre d'affaires mensuel ou les cours mensuels des actions sur plusieurs années, les résultats peuvent être faux en raison de l’apparition possible de corrélations trompeuses. Imaginez un éditeur de logiciels cherchant à modéliser ses revenus en fonction d'autres facteurs, en se basant sur des données mensuelles sur l'année écoulée. Dans le cas où les revenus ont augmenté mois après mois, ils sont susceptibles d’être corrélés avec toute variable aléatoire montrant une augmentation d'un mois à l'autre au cours de la dernière année, y compris des variables qui n'ont théoriquement aucun lien avec le logiciel. Exemples : les précipitations ou les taux de criminalité ou les admissions dans une université spécifique... Les variables présentant une tendance temporelle doivent donc être transformées.

En plus de l'absence de tendance, d'autres propriétés des séries temporelles doivent être vérifiées avant utilisation dans des modèles de régression. Ces propriétés comprennent une variance constante et l'absence de motifs saisonniers ou plus généralement cycliques. De plus, la série temporelle ne doit pas correspondre à une marche aléatoire. Une série temporelle respectant toutes ces propriétés est une série stationnaire. La stationnarité peut être testée à l'aide de tests de racine unitaire et de stationnarité, notamment les tests Augmented Dickey-Fuller, Phillips-Perron ainsi que KPSS.

Voici quelques transformations de séries temporelles qui permettent de les rapprocher de la stationnarité lorsque c’est nécessaire.

b. Atteindre la stationnarité : éliminer les tendances et la saisonnalité grâce à la différenciation

Une façon de supprimer la tendance dans les variables dépendantes ou indépendantes consiste à différencier les séries en question. Il s’agit de calculer la différence de chaque donnée avec la donnée précédente. Dans le cas des revenus mensuels, cela correspondrait à l'utilisation de la différence entre chaque revenu et le revenu du mois précédent. La différenciation peut également être exécutée à l'échelle saisonnière pour supprimer la saisonnalité, cette dernière pouvant également conduire à des corrélations trompeuses.

D'une certaine manière, cette procédure permet de supprimer une éventuelle autocorrélation sérielle parmi les résidus du modèle. L’autocorrélation sérielle peut être testée grâce au test de Durbin-Watson. Néanmoins, dans le cas de données sériellement autocorrélées, on peut également utiliser le modèle de Cochrane-Orcutt sur les données d’origine. Il s'agit d'un modèle de régression intégrant une correction de l’autocorrélation sérielle.

c. Atteindre la stationnarité : obtenir une variance constante

Dans de nombreuses procédures de modélisation et de prédiction telles que la régression linéaire ou les modèles ARIMA, il est conseillé de travailler sur des séries temporelles à variance constante. Pour vérifier si la variance d’une série temporelle est constante, on peut avoir recours aux tests d'hétérogénéité tels que les tests de Breusch-Pagan ou de White. Ces tests sont par ailleurs souvent exécutés sur les résidus d'un modèle de régression pour tester l'hypothèse d’homoscédasticité.

Certaines transformations de séries chronologiques telles que le logarithme ou la transformation de Box-Cox contribuent à rendre la variance plus homogène. La transformation Box-Cox peut se trouver dans la fonctionnalité transformation de série temporelle.

d. Existe-t-il un lien entre plusieurs séries temporelles sur le long terme ?

Les tests de cointégration peuvent être utilisés pour vérifier si plusieurs séries temporelles partagent une tendance stochastique sous-jacente les conduisant à un équilibre sur le long terme. Ils sont souvent utilisés en finance pour étudier les relations entre différents taux de change.

Comment prévoir les valeurs futures d'une série temporelle ?

L’analyse de séries temporelles a souvent pour objectif la prédire des valeurs futures d'une variable spécifique. Par exemple, les grossistes cherchent à prédire le nombre d'articles susceptibles d'être vendus dans le mois à venir pour adapter les stocks dans leurs entrepôts. Les météorologistes prédisent la température et les précipitations des jours suivants.

De nombreuses méthodes de prédiction existent. Les principales méthodes disponibles dans XLSTAT sont comparées ci-dessous. Toutes fournissent des intervalles de confiance mesurant le degré d'incertitude de la prédiction.

a. Prédire avec la régression linéaire

Une fois l’équation d’une régression linéaire établie, elle peut être utilisée pour prédire les valeurs de la variable dépendante en fonction de nouvelles valeurs des variables indépendantes. Ces valeurs peuvent être réelles ou inspirées d'un scénario futur. Par exemple, les revenus peuvent être prédits sur la base de scénarios hypothétiques impliquant des valeurs spécifiques de cours d’actions ou d’investissements marketing. Pour obtenir des prédictions à partir d’une régression dans XLSTAT, utilisez l'onglet Prédiction de la boîte de dialogue de régression linéaire.

b. Prédire avec le lissage exponentiel

Les méthodes de lissage exponentiel permettent de prédire une série temporelle seule, c’est-à-dire sans prendre en compte des variables indépendantes. Elles se basent sur l'idée que les valeurs les plus récentes devraient avoir le poids maximal pour déterminer les prédictions. Plusieurs méthodes existent et se trouvent dans la fonctionnalité de lissage XLSTAT :

• Lissage exponentiel simple : toutes les prédictions ont la même valeur, qui n’est autre qu’une moyenne pondérée des données passées, avec des poids décroissant vers les valeurs passées
• Lissage exponentiel double : ajoute une tendance linéaire à la prédiction.
• Lissage Holt-Winters linéaire : similaire au lissage exponentiel double, mais plus flexible car il implique un paramètre supplémentaire.
• Lissage Holt-Winters saisonnier additif : prend en compte une composante saisonnière.
• Lissage Holt-Winters saisonnier multiplicatif : prend en compte la saisonnalité ainsi qu’une variance changeante.

c. Prédire avec le modèle ARIMA

Les modèles ARIMA sont une famille de méthodes statistiques permettant de modéliser et de prédire une série temporelle à partir de ses propres valeurs passées et tout en incorporant (optionnellement) les informations de variables indépendantes. Le modèle ARIMA comprend les composantes suivantes :

• AR (AutoRegressive) : une donnée au temps t est prédite à partir d’une régression sur des séries décalées dans le passé (t-1, t-2…).
• MA (Moving Average) : une donnée au temps t est prédite à partir erreurs de prédictions passées.

ARIMA permet une différenciation automatique des séries temporelles. C'est ce que représente le I (Intégré) dans ARIMA. Il est également possible de configurer une différenciation saisonnière.

ARIMA implique plusieurs paramètres à calibrer, tels que l'ordre des composantes AR et MA, l’ordre de différenciation, ainsi que les paramètres liés à la saisonnalité. Pour choisir les valeurs optimales des paramètres, une solution est d’effectuer une sélection automatique se basant sur l'optimisation d’indices tels que AICc ou SBC. Les utilisateurs avancés peuvent également avoir recours aux fonctions d'autocorrélation (ACF) et d'autocorrélation partielle (PACF) pour déterminer un ensemble approprié de valeurs de paramètres. Ces fonctions peuvent être obtenues à l'aide de la fonctionnalité d'analyse descriptive des séries temporelles.

Comment mesurer les cycles dans une série temporelle ?

L'analyse spectrale permet de mesurer les périodes de cycles potentiels dans une série temporelle. En d'autres termes, elle aide à estimer le domaine fréquentiel de la série. XLSTAT fournit également une fonctionnalité de Fourier, qui permet d’effectuer des transformées de Fourier et des transformées inverses, en intégrant plusieurs améliorations par rapport à la fonction Excel standard de transformée de Fourier.