Test d'homogénéité d'une série temporelle dans Excel
Jeu de données pour réaliser un test d'homogénéité d'une série temporelle
Une feuille Excel contenant les données et les résultats de cet exemple peut être téléchargée.
Les données proviennent du relevé du débit d’une rivière durant 30 jours. Le but est ici de vérifier qu’une série temporelle est homogène entre deux temps donnés.
La variété des tests utilisés vient de ce que les hypothèses alternatives possibles sont nombreuses : changement de distribution, changements de moyenne (une ou plusieurs fois) ou présence de tendance.
Les tests disponibles dans XLSTAT correspondent à l’hypothèse alternative d’un unique décalage. Pour l’ensemble des tests, XLSTAT fournit des p-values en utilisant des rééchantillonnages Monte Carlo, les calculs exacts étant soit impossibles soit trop coûteux en temps de calcul.
Paramétrer un test d'homogénéité d'une série temporelle
Une fois XLSTAT lancé, cliquez sur l’icône TIME et choisissez la fonction Tests d’homogénéité.

Une fois le bouton cliqué, la boîte de dialogue apparaît. Vous pouvez alors sélectionner les données sur la feuille Excel.
Vous devez sélectionner la série temporelle "débit".
L'option Libellé des séries est laissée activée car la première ligne de la colonne de données comprend le nom de la série.
Nous sélectionnons la première colonne comme données de date, celle-ci représente le jour dans le mois.
Nous allons appliquer quatre tests. Le test de Pettitt, le test SNHT (Standard normal homogeneity test), le test de Buishand et le rapport de von Neumann.

Dans les options, l’hypothèse alternative est prise telle que le décalage est différent de 0, c’est-à-dire qu’il existe un décalage entre deux parties de la série temporelle.

Une fois que vous avez cliqué sur le bouton OK, les calculs sont effectués, puis les résultats sont affichés.
Interpréter les résultats d'un test d'homogénéité d'une série temporelle
XLSTAT vous donne d’abord des statistiques descriptives pour la série sélectionnée. Ensuite, les résultats des tests sont affichés.
Le test de Pettitt est un test non paramétrique ne nécessitant aucune hypothèse quant à la distribution des données. Le test de Pettitt est une adaptation du test de Mann-Whitney basé sur les rangs, permettant d’identifier le temps auquel se produit un changement.

La p-value indique clairement qu’on rejette l’hypothèse nulle et donc qu’on peut considérer qu’il existe un décalage entre deux parties de cette série temporelle. Le graphique associé montre très bien ce décalage.

Le test SNHT (Standard normal homogeneity test) se base sur l’hypothèse nulle que les rapports centrés réduits entre la valeur observée de la série et la moyenne suivent une distribution N(0,1). La p-value obtenue est inférieure à 0,0001 et l’hypothèse nulle est donc rejetée. On peut donc dire que entre les temps 1 et n les variables sont distribuées suivant une loi N(µ1, 1) et entre n+1 et T elles sont distribuées suivant une loi N(µ2,1). Ces conclusions confirment celles du premier test.

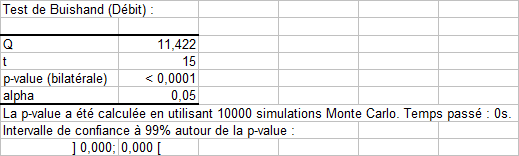
Le test de Buishand se base sur l’hypothèse nulle que les variables suivent une ou plusieurs distributions ayant une même moyenne. La p-value obtenue est inférieure à 0,0001 et l’hypothèse nulle est donc rejetée. On peut donc dire qu’il existe un temps t à partir duquel les variables changent de moyenne. Les conclusions précédentes sont aussi validées.
Finalement, le rapport de von Neumann est basé sur la somme des carrés des différences entre deux valeurs successives de la série. L’espérance de ce rapport est de 2 lorsque la moyenne est constante. La p-value est de 0,002 et on rejette donc l’hypothèse nulle qui suppose que les données sont homogènes. Ce résultat est cohérent avec les résultats précédents.

Cette courte analyse nous a montré que les tests d’homogénéité ont tous rejeté l’hypothèse nulle d’homogénéité de la série temporelle. Ainsi, il existe un point au-delà duquel le débit de cours d’eau est différent. Ce point se situe au niveau du 15ème jour du mois.
Cet article vous a t-il été utile ?
- Oui
- Non