Zeitreihen auf Homogenität testen - Anleitung

Dieses Tutorium zeigt Ihnen, wie Sie einen Homogenitätstest auf einer Zeitreihe in Excel mithilfe der Statistiksoftware XLSTAT einrichten und interpretieren.

Datensatz für den Homogenitätstest einer Zeitreihe

Was sind Homogenitätstests einer Zeitreihe?

Die Homogenitätstests setzen sich aus einer Vielzahl an Tests zusammen, bei denen die Nullhypothese ist, dass eine Zeitreihe zwischen zwei gegebenen Zeitpunkten homogen ist.Die Bandbreite der Tests beruht auf der Tatsache, dass die möglichen alternativen Hypothesen zahlreich sind: Änderung der Verteilung, Änderung des Mittelwertes (ein oder mehrmals) oder Vorhandensein einer Tendenz.

Die in diesem Tool vorgestellten Tests entsprechen alle der alternativen Hypothese einer einmaligen Verschiebung. Für alle Tests stellt XLSTAT p-Values unter Verwendung von Monte Carlo Simulationen bereit, weil die exakten Berechnungen entweder nicht möglich oder zeitlich zu umfangreich sind.

Einrichten eines Homogenitätstests einer Zeitreihe

Nach dem Öffnen von XLSTAT, klicken Sie auf den Button "Zeitreihen" im Ribbon und wählen “Homogenitätstest” (siehe unten).

Nach dem Klicken des Buttons erscheint das entsprechende Dialogfenster. Sie können nun die Daten im Excel-Blatt auswählen. Es muss die Zeitreihe „Fluss“ ausgewählt werden. Wählen Sie die ersten 5 Kontingenztabellen (jede entspricht einem Niveau an Penicillin). Die Option "Spaltenbeschriftung" ist aktiviert, da die erste Zeile der Auswahl die Namen der Variablen enthält. Die Daten sind in der ersten Spalte. Sie entsprechen den Tagen des Monats. Vier Tests können angewendet werden: Der Pettitt Test, Alexandersson SNHT Test, Buishand Test und der von Neumann Verhältnistest.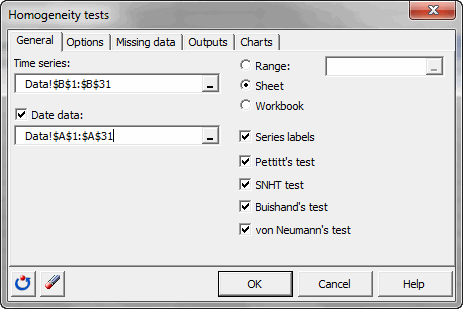

Im Reiter "Optionen" wird die Verschiebung <> 0 als alternative Hypothese ausgewählt. Dies bedeutet, dass eine Verschiebung zwischen den beiden Teilen der Zeitreihe existiert.

Die Berechnungen beginnen, sobald der OK Button geklickt wurde.

Interpretieren der Ergebnisse eines Homogenitätstests einer Zeitreihe

Die Ergebnisse werden angezeigt. XLSTAT zeigt als erstes eine Tabelle mit einfachen Statistiken, die die Zeitreihe beschreiben.

Dann wird das Ergebnis des ersten Tests angezeigt.

Der Pettitt Test ist ein nicht-parametrischer Test, der keine Hypothese über die Verteilung der Daten unterstellt. Der Pettitt Test ist eine Anpassung des Mann-Whitney Tests, der auf den Rängen basiert, und der das Identifizieren des Zeitpunkts der Verschiebung erlaubt.

Die p-values zeigen, dass die Nullhypothese zurückgewiesen werden kann. Man kann schließen, dass eine Verschiebung zwischen zwei Teilen der Zeitreihe existiert. Das zugehörige Diagramm bestätigt das Ergebnis.

Der SNHT Test (Standard normal homogeneity test) wird auf eine Reihe von Verhältnissen angewandt. Die Verhältnisse werden anschießend zentriert und reduziert. Die Nullhypothese ist H0: Alle T Variablen Xi folgen einem Gesetz N(0,1).

Da der p-value sehr klein ist, kann die Nullhypothese zurückgewiesen werden. Man kann schließen, dass eine Verschiebung zwischen zwei Teilen der Zeitreihe existiert. Dieses Ergebnis bestätigt das Ergebnis des ersten Tests.

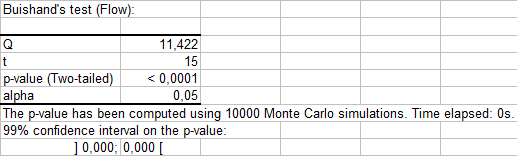
Der Buishand (1982) Test kann auf Variablen angewandt werden, die beliebigen Verteilungen folgen. Die Nullhypothese ist H0: Die T Variablen folgen einer oder oder mehreren Verteilungen mit dem gleichen Mittelwert. Da der p-value sehr klein ist, kann die Nullhypothese zurückgewiesen werden. Die alternative Hypothese ist, dass es ein Zeitpunkt t gibt, ab dem die Variablen den Mittelwert wechseln.

Das von Neumann Verhältnis basiert auf den Summen der quadrierten Differenzen zwischen allen Paaren aufeinanderfolgender Zeitpunkte. Der Mittelwert dieses Verhältnisses ist gleich 2, wenn der Mittelwert der Zeitreihe konstant ist. Der p-value ist gleich 0,002, die Nullhypothese der Homogenität der Zeitreihe wird daher zurückgewiesen. Dies bestätigt die vorhergehenden Ergebnisse.

Man kann mit diesen Tests zeigen, dass eine Verschiebung im Fliessen des Flusses vorliegt, der sich am 15ten Tag des Monats ereignet.