Time series homogeneity test in Excel tutorial
This tutorial will help you set up and interpret a homogeneity test on a time series in Excel using the XLSTAT statistical software.
Dataset for the homogeneity test of a time series
Data are measures of the flow of a river taken every day during one month (30 measures). Our goal is to check if this time series is homogenous.
Homogeneity tests of a time series
Homogeneity tests involve a large number of tests for which the null hypothesis is that a time series is homogenous between two given times. The variety of the tests comes from the fact that there are many possible alternative hypotheses: change in distribution, changes in average (one or more times) or presence of trend.
The tests presented in this tool correspond to the alternative hypothesis of a single shift. For all tests, XLSTAT provides p-values using Monte Carlo resamplings. Exact calculations are either impossible or too costly in computing time.
Setting up a homogeneity test of a time series
After opening XLSTAT, click the Time button in the ribbon and select Homogeneity tests (see below).

Once you've clicked on the button, the dialog box appears.
Select the data on the Excel sheet. You have to select the time series “flow”.
As we selected the column title for the series, we leave the option Series labels activated. The dates are in the first column, they correspond to days of the month.
Four tests can be applied: The Pettitt's test, Alexandersson’s SNHT test, Buishand’s test and von Neumann’s ratio test. 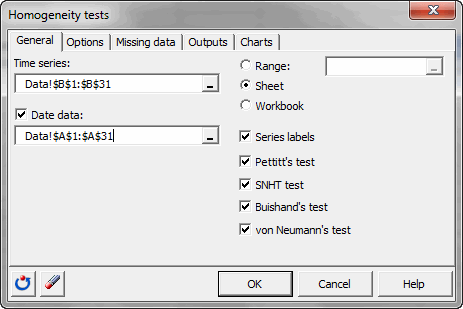
In the Options tab, we select Shift <> 0 as alternative hypothesis. It means that there is a shift between two parts of the time series.

Once you have clicked on the OK button, the computation starts.
Interpreting the results for a homogeneity test of a time series
The results start with the basic statistics associated to the time series.
Then, the results of the first test are displayed. The Pettitt's test is a nonparametric test that requires no assumption about the distribution of data. The Pettitt's test is an adaptation of the rank-based Mann-Whitney test that allows identifying the time at which the shift occurs.

The p-value shows that the null hypothesis is rejected; we can conclude that there is a shift between two parts of our time series. The associated plot confirms this result.

The SNHT test (Standard Normal Homogeneity Test) is usually applied to a series of ratios that compare the observations with an average. The ratios are then standardized. The null hypotheses is: H0: The obtained ratios follow a N(0,1) distribution.
Since the p-value is very small, we reject the null hypothesis and thus conclude that there exists a shift in the time series. This result confirms the result of the first test.

The Buishand’s test (1982) can be used on variables following any type of distribution. It is based on the null hypothesis: H0: The T variables follow one or more distributions that have the same mean. Since the p-value is very small, this hypothesis is rejected and the alternative hypothesis will be: there exists a time t from which the variables change of mean.
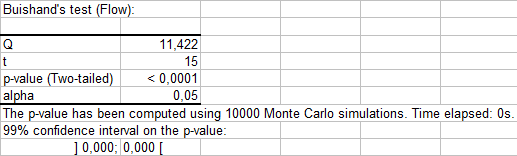
Finally, the von Neumann ratio is based on the sum of the squares differences between each pair of following time measures. The mean of this ratio is equal to 2 when the average of the time series is constant. The p-value is equal to 0,002, which leads us to reject the null hypothesis of homogeneity of the time series. This also confirms the preceding results.

We have shown with these test that there exists a shift in the flow of the river that happens at the 15th day of the month.
Was this article useful?
- Yes
- No