Prueba homogeneidad series temporales Excel

Este tutorial le mostrará cómo configurar e interpretar una prueba de homogeneidad sobre una serie de tiempo en Excel usando el software estadístico XLSTAT.

Datos para la prueba de homogeneidad de una serie temporal

Los datos son medidas de la corriente de un río tomadas todos los días durante un mes (30 medidas). Nuestro objetivo es comprobar si esta serie de tiempo es homogénea.

Pruebas de homogeneidad de una serie temporal

Las pruebas de homogeneidad implican un gran número de ensayos para los que la hipótesis nula es que una serie de tiempo es homogénea entre dos momentos dados. La variedad de las pruebas viene del hecho de que hay muchas posibles hipótesis alternativas: cambio en la distribución, cambios en la media (una o más veces) o presencia de una tendencia. Las pruebas presentadas en esta herramienta corresponden a la hipótesis alternativa de un solo turno (single shift). Para todas las pruebas, XLSTAT proporciona los valores p utilizando remuestreos Monte Carlo. Los cálculos exactos son o imposibles o demasiado costosos en tiempo de cálculo.

Configuración de una prueba de homogeneidad de una serie temporal

Una vez abierto XLSTAT, haga clic en el comando Análisis de series temporales, y seleccione Pruebas de homogeneidad (véase siguiente captura de pantalla).

Una vez haya hecho clic en el botón, aparece el cuadro de diálogo.

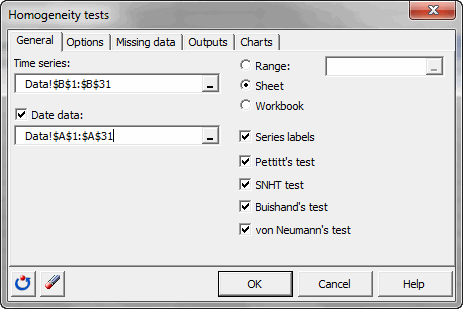
Seleccione los datos en la hoja de cálculo de Excel. Tiene que seleccionar la serie de tiempo “flow”.

Puesto que hemos elegido el título de la columna para la serie, dejamos activada la opción Etiquetas de la serie. Los Datos de fecha están en la primera columna, y corresponden a los días del mes.

Se pueden aplicar cuatro pruebas: La prueba de Pettitt, prueba SNHT de Alexandersson, la prueba de Buishand y prueba de razón de von Neumann.

En la pestaña Opciones, seleccionamos Cambio <> 0 como Hipótesis alternativa. Esto significa que hay un cambio (shift) entre dos partes de la serie de tiempo.

Una vez haya hecho clic en el botón OK, se inicia el cómputo.

Interpretación de los resultados de una prueba de homogeneidad de una serie temporal

Los resultados comienzan con los estadísticos básicos asociados a la serie de tiempo.

A continuación, se muestran los resultados de la primera prueba. La prueba de Pettitt es una prueba no paramétrica que no requiere ninguna aunción sobre la distribución de los datos. La prueba de Pettitt es una adaptación de la prueba de Mann-Whitney basada en rangos, que permite identificar el momento en que se produce el cambio.

El valor p indica que se rechaza la hipótesis nula; podemos concluir que hay un cambio entre dos partes de nuestra serie de tiempo. El gráfico asociado confirma este resultado.

La prueba de homogeneidad normal estándar SNHT (Standard Normal Homogeneity Test) se aplica generalmente a una serie de ratios que comparan las observaciones con un promedio. Las ratios son entonces estandarizadas. La hipótesis nula es: H0: Las relaciones obtenidas siguen una distribución N(0,1).

Dado que el valor de p es muy pequeño, se rechaza la hipótesis nula y, por lo tanto, concluimos que existe un cambio en la serie temporal. Este resultado confirma el resultado de la primera prueba.

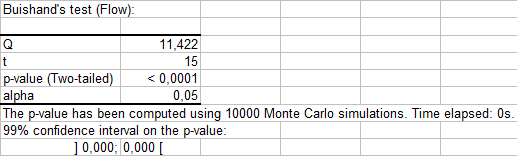
La prueba de Buishand (1982) se puede utilizar sobre variables que siguen cualquier tipo de distribución. Se basa en la hipótesis nula: H0: Las variables T siguen una o más distribuciones que tienen la misma media. Dado que el valor de p es muy pequeño, esta hipótesis es rechazada y la hipótesis alternativa será: no existe un tiempo t desde el que las variables cambian de media.

Por último, le ratio de von Neumann se basa en la suma de las diferencias al cuadrado entre cada par de las siguientes medidas de tiempo. La media de esta ratio es igual a 2 cuando la media de la serie de tiempo es constante. El valor de p es igual a 0.002, lo que nos lleva a rechazar la hipótesis nula de homogeneidad de las series de tiempo. Esto también confirma los resultados anteriores.

Hemos mostrado con estas pruebas que existe un cambio en el flujo del río que sucede en el día 15 del mes.