Usar diferencias para obtener series temporales estacionales
Este tutorial le mostrará cómo describir una serie de tiempo y transformarla para que se convierta en estacionaria, en Excel usando el software XLSTAT.
Datos para la transformación de diferenciación
Los datos se han obtenido de [Box, G.E.P. and Jenkins, G.M. (1976). Time Series Analysis: Forecasting and Control. Holden-Day, San Francisco], y corresponden a los pasajeros mensuales (en miles) de líneas aéreas internacionales desde enero de 1949 hasta diciembre de 1960. Se utiliza ampliamente como serie temporal estacional no estacionaria. Nuestro objetivo es mostrar cuán útil puede ser un análisis descriptivo antes de llevar a cabo una aproximación de modelado.

Nos percatamos de que existe una tendencia global ascendente en el gráfico. Cada año, un ciclo similar se inicia mientras que la variabilidad dentro de un año parece aumentar con el tiempo. Con el fin de confirmar esta tendencia vamos a analizar la función de autocorrelación de la serie.
Configuración de un análisis descriptivo de series temporales
Una vez abierto XLSTAT, seleccione el comando XLSTAT / Análisis de series temporales / Análisis descriptivo.

Una vez haya hecho clic en el botón, aparece el cuadro de diálogo Análisis descriptivo. Seleccione los datos en la hoja de cálculo de Excel. Las Series temporales corresponden a la serie de interés, los Pasajeros. Activamos la opción Etiquetas de las series debido a que la primera fila de los datos seleccionados contiene el encabezado de la variable.

En la pestaña Opciones, seleccionamos la opción Automático en el cuadro Pasos de tiempo:

Las pestañas Resultados y Gráficos se han configurado de la siguiente manera:


Los cálculos empiezan una vez haya hecho clic en OK. Se muestran a continuación los resultados.
Interpretación de los estadísticos descriptivos de una serie temporal
La primera tabla muestra el resumen de estadísticos. A continuación se muestra la tabla de prueba de Normalidad y pruebas de ruido blanco. La prueba de Jarque-Bera es una prueba de normalidad, basada en los coeficientes de asimetría y curtosis. Cuanto mayor sea el valor del estadístico Chi-cuadrado, más improbable es la hipótesis nula de que los datos se distribuyen normalmente. Aquí el valor de p, que corresponde a la probabilidad de equivocarse al rechazar la hipótesis nula, es cercano a 0.012. Con un nivel de significación alfa = 0.05, se debe rechazar la hipótesis nula.
Las otras tres pruebas (Box-Pierce, Ljung-Box, McLeod-Li) se calculan a diferentes retardos de tiempo. Permiten probar si los datos podrían ser asumidos como ruido blanco o no. Estas pruebas también se basan en la distribución Chi-cuadrado. Todas coinciden en que no se puede asumir que los datos sean generados por un proceso de ruido blanco. En tanto que la clasificación de los datos no tiene ninguna influencia en la prueba de Jarque-Bera, sí tiene influencia en las otras tres pruebas, que son particularmente adecuadas para el análisis de series de tiempo.

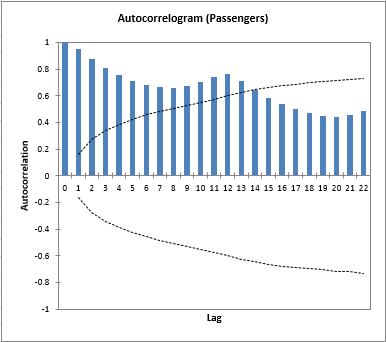
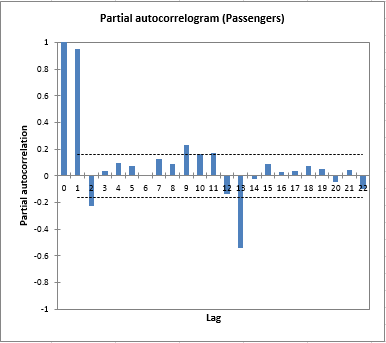
Por debajo de la tabla que muestra las funciones descriptivas de las series de tiempo, dos gráficos de barras muestran la evolución de la función de autocorrelación (autocorrelation function, ACF) y de la función de autocorrelación parcial (partial autocorrelation function, PACF). También se muestran los intervalos de confianza al 95%. Al observar el autocorrelograma, podemos identificar una clara autocorrelación de retardo 1, así como una estacionalidad, que parece ser de 12 meses.
Transformación de una serie temporal
Con el fin de mejorar la normalidad de los datos, queremos realizar dos transformaciones: En primer lugar, queremos estabilizar la variabilidad en aumento de la serie. En segundo lugar, queremos eliminar las autocorrelaciones diferenciando la serie.
Configuración de la transformación de una serie temporal
Esto se puede hacer utilizando la herramienta Transformación de series de tiempo. Para activar el correspondiente cuadro de diálogo, seleccione el comando XLSTAT / Análisis de series temporales / Transformación de series de tiempo, o bien haga clic en el botón correspondiente de la barra de herramientas (véase siguiente captura de pantalla).

Una vez haya hecho clic en el botón, aparece el cuadro de diálogo.
Seleccione los datos en la hoja de cálculo de Excel. Las Series temporales corresponden a la serie de interés, los pasajeros (“Passengers”).

Después de haber seleccionado los datos, seleccione la opción de Transformación Box-Cox en la pestaña Opciones.
Tenemos la posibilidad de solicitar una transformación optimizada (debería ajustarse el parámetro lambda de la transformación Box-Cox de modo que la probabilidad de un modelo de regresión - Y transformada = función lineal simple de tiempo - fuera lo más alta posible). Sin embargo, decidimos aquí fijar el valor de lambda a 0, que corresponde a una transformación logarítmica de la serie.
La transformación logarítmica es a menudo una buena opción para eliminar la creciente variabilidad.

Los cálculos empiezan una vez haya hecho clic en OK.
Resultados de la transformación de una serie temporal
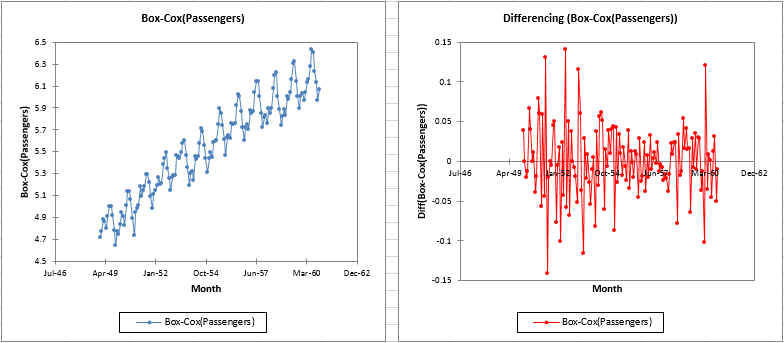
Primero vemos una tabla y dos gráficos: uno para el conjunto de datos original y el otro para la transformación de Box-Cox. Como era de esperar, la transformación logarítmica ha eliminado la variabilidad cada vez mayor.

A continuación, con el fin de eliminar la tendencia y el componente estacional, decidimos utilizar el método de diferenciación. Primero seleccionamos la serie transformada de Box-Cox en la nueva hoja.

Fijamos el valor de d en 1 para eliminar la tendencia, y D y s en 1 y 12 para eliminar componente estacional de los 12 meses.

El gráfico resultante muestra que la transformación de diferenciación ha eliminado efectivamente la tendencia.
Estadísticos descriptivos en series de tiempo transformadas
Podemos comprobar ahora si la serie diferenciada es ruido blanco mediante la aplicación de nuestro análisis descriptivo, una vez más, como se muestra en la figura.

Puesto que el método de diferenciación ha creado algunos valores perdidos, deberíamos decidir cómo manejarlos. En la pestaña Datos perdidos, activamos la opción Eliminar las observaciones.

La prueba de Jarque-Bera confirma que la serie se acerca a una muestra normal (hemos pasado de 0.012 a 0.027), pero permanece no estacionaria según lo confirmado por las pruebas de ruido blanco.

Las transformaciones no han sido suficientemente eficaces. De hecho, el autocorrelograma indica que algún componente significativo permanece en los retardos 1 y 12. Se necesitan otras investigaciones con el fin de entender el fenómeno subyacente.

Descomposición estacional de las series
Otro enfoque para explorar nuestra serie de tiempo sería descomponerla primero en componente identificado mediante la opción Descomposición estacional de la herramienta de transformación. Así que empezamos de nuevo a partir de los datos originales como se muestra en la siguiente figura.

Esta vez, seleccionamos Descomposición estacional en la pestaña Opciones. Parece apropiado un modelo multiplicativo, dado que la serie de tiempo exhibe un comportamiento multiplicativo claro en la escala natural. El período se establece en 12 para una periodicidad de 1 año sobre datos mensuales.

Una vez calculada, la descomposición se visualiza a través de 4 gráficos: la serie original, un componente de tendencia, un componente estacional y un componente aleatorio. Las 3 últimas se pueden multiplicar entre sí con el fin de reconstruir la serie original.

En este momento podríamos comprobar la estacionalidad del componente aleatorio. Sin embargo, podemos transformar antes este componente aleatorio utilizando la transformación de Box-Cox (transformación log) de modo que esté centrado en 0.

Véase la serie resultante que se muestra en la hoja.

El análisis descriptivo se pone en marcha otra vez en esta serie.

Esta vez la prueba de Jarque-Bera no permite rechazar la hipótesis de una variable distribuida normalmente.

Por desgracia, un patrón estacional, menos significativo que antes, sigue siendo visible en el autocorrelograma. Esto volvería a suponer un trabajo adicional en el proceso de generación.

¿Ha sido útil este artículo?
- Sí
- No