Prueba de cointegración en series temporales Excel

Este tutorial le mostrará cómo configurar e interpretar pruebas de cointegración sobre series de tiempo en Excel usando el software estadístico XLSTAT.

Datos para ejecutar una prueba de cointegración

Este tutorial utiliza un conjunto de datos extraídos de la base de datos facilitados por el Bank of England. Se compone de dos series de tiempo:
-El Tipo medio mensual de cambio a plazo de 12 meses de US$ en libras esterlinas, etiquetada como XUMADSY,
-El Tipo medio mensual de cambio al contado de US$ en libras esterlinas, etiquetada como XUMAUSS.
Ambas series cubren un período de tiempo que va desde enero 1979 hasta diciembre de 1999.

Objetivo de este tutorial

El tipo de cambio expresa el precio de una moneda, la extranjera, en términos de otra, la doméstica. En nuestro tutorial, vamos a considerar los tipos de cambio a 12 meses de plazo y al contado del dólar estadounidense en términos de la libra esterlina durante el período 1979-1999. Por un lado, el tipo de cambio a plazo para los próximos 12 meses es un contrato de cobertura en el que dos partes están de acuerdo en el momento presente sobre el tipo al que se intercambiarán las dos monedas en el futuro (12 meses antes). Por otro lado, el tipo de cambio al contado fija el valor relativo actual de las dos monedas.
En el contexto de la paridad de interés cubierto (Covered Interest Parity, CIP), se espera que el registro de los tipos de cambio al contado y a plazo estén relacionados con el diferencial exterior con respecto al doméstico de los tipos de interés mediante la siguiente relación:
lnForward - lnSpot = rDiff.
donde lnForward es el logaritmo del tipo de cambio a plazo, lnSpot es el logaritmo del tipo de cambio al contado y rDiff es el tipo de interés diferencial.
Según la hipótesis de los mercados financieros eficientes, no debería ser posible una situación de beneficios “sin riesgos” (libre de riesgos) en la que uno podría recibir un préstamo en una divisa extranjera, invertir a un tipo de cambio “sin riesgo” en esa divisa y blindar su precio de venta en la divisa nacional en una venta futura. Como consecuencia de esto, se espera que el diferencial del tipo de interés sea I(0) ( o fijo). Como es un hecho generalmente aceptado en la literatura financiera internacional que tanto los tipos de cambio al contado como los que son a término (futuro) estén integrados en la secuencia 1 (es decir I (1)), debería existir una relación de cointegración entre los registros de los tipos de cambio al contado y a término (futuro) para mantener la relación de Paridad entre el Precio al Contado y el Precio a Término (futuro).
En el siguiente tutorial, debemos transformar nuestra primera serie de tiempo y probar su estado I(1). A continuación, deberíamos evaluar que los dos procesos I(1) se pueden combinar a un proceso I(0); en otras palabras, que las dos series temporales están cointegradas, por medio de una prueba de cointegración que sigue la aproximación de Johansen.

Transformación de series temporales

En primer lugar, tenemos que transformar la serie extraída de la base de datos del Banco de Inglaterra para obtener sus valores log. Una vez abierto XLSTAT, seleccione el comando Análisis de series temporales / Transformación de series de tiempo (véase siguiente captura de pantalla).

Aparece el cuadro de diálogo de Transformación de series de tiempo como se muestra a continuación. Seleccione la serie de tiempo en la hoja de cálculo de Excel.

Se deja activada la opción Etiquetas de la serie, puesto que la primera fila de los datos seleccionados contiene las cabeceras de las variables.

En la pestaña Opciones, seleccione la Transformación Box-Cox y fije el valor de Lambda de 0 para aplicar una transformación logarítmica a la serie:

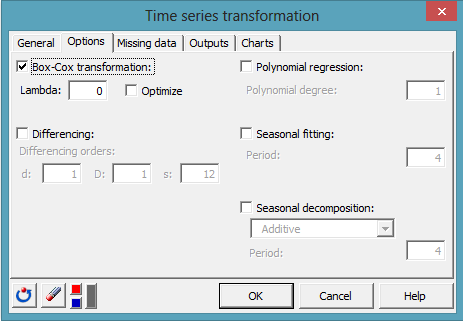
Una vez se hace clic en OK, se realizan los cálculos y las dos series transformadas se muestran en una nueva hoja.

En primer lugar, el tipo de cambio a plazo de 12 meses (XUMADSY) y su transformación logarítmica (Box-Cox (XUMADSY))...

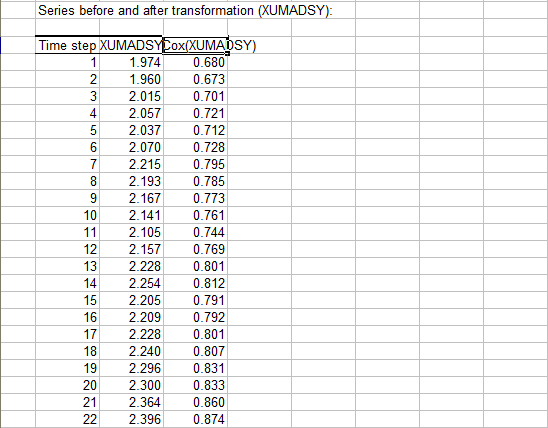
...seguido del tipo de cambio al contado (XUMAUSS) y su transformación logarítmica (Box-Cox (XUMAUSS)):

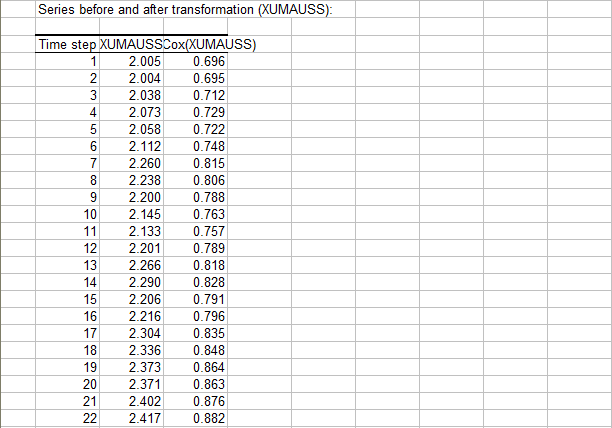
Análisis descriptivo

Ahora que nuestras series de tiempo están listas, debemos aplicar un análisis descriptivo sobre ellas con el fin de controlar que presentan las características esperadas.

Para llevar a cabo un análisis descriptivo, haga clic en el comando Análisis de series temporales / Análisis descriptivo, como se muestra a continuación.

Seleccione las dos serie transformada, Box-Cox(XUMADSY) y Box-Cox(XUMAUSS), con la ayuda de la tecla Ctrl para seleccionar varios campos:

En la pestaña Resultados, asegúrese de que están activadas las opciones Autocorrelaciones y Autocorrelaciones parciales como se muestra a continuación.

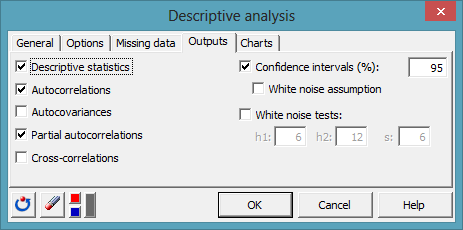
En la pestaña Gráficos, active las opciones Autocorrelograma (ACF) y Autocorrelograma parcial (FAP):

Una vez haya hecho clic en OK, se muestran los estadísticos descriptivos, así como el ACF y PACF para las dos series.
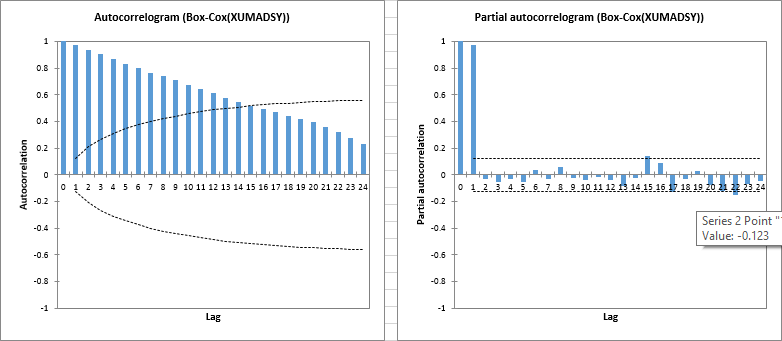
En primer lugar, como se muestra a continuación, la ACF de la serie Box-Cox(XUMADSY) exhibe un gran número de retardos significativos.
En cuanto a la PACF, parece que esas correlaciones de orden superior se explican principalmente por la autocorrelación de retardo 1, ya que es la única fuertemente significativa en la PACF.
Este comportamiento es bastante compatible con la serie de tiempo I(1) esperada.

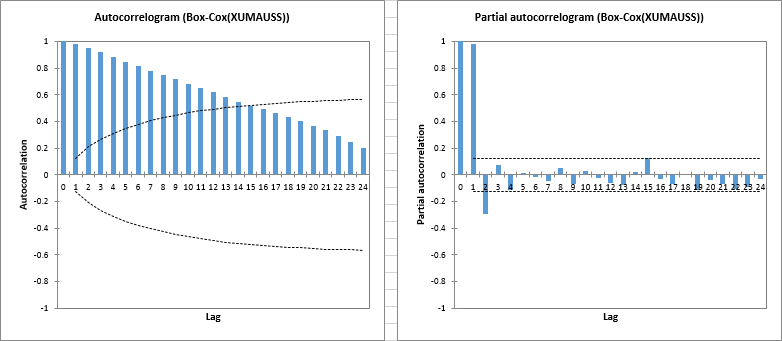
La situación es muy similar para la segunda serie de tiempo llamada Box-Cox(XUMAUSS) como se muestra a continuación con un retardo-1 fuertemente significativo en la PACF.

Pruebas de raíz unitaria (unit root tests)

Después de esas comprobaciones preliminares, estamos listos para probar el aspecto I(1) de nuestra serie de tiempo. Vamos a aplicar dos pruebas de raíz unitaria a nuestra serie temporal transformada: una prueba de Dickey-Fuller (DF) y una prueba de Phillips-Perron (PP).

Seleccione Análisis de series temporales / Pruebas de raíz unitaria y de estacionariedad, como se muestra a continuación.

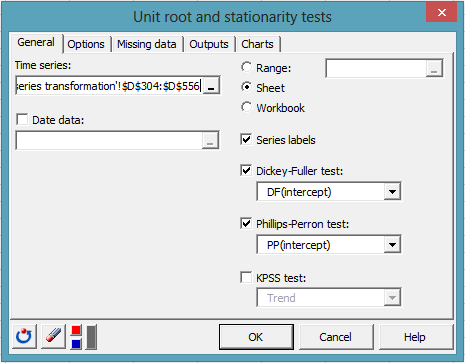
En el campo Series temporales, seleccione las dos series transformadas, Box-Cox(XUMADSY) y Box-Cox(XUMAUSS), y active la pruebas de Phillips-Perron y Dickey-Fuller como se muestra a continuación.
En cuanto a la selección del modelo, el modelo con una intercepta es el que mejor describe nuestros datos. Por lo tanto, deberíamos seleccionar la opción de intercepción, tanto para la prueba DF como para la prueba PP.

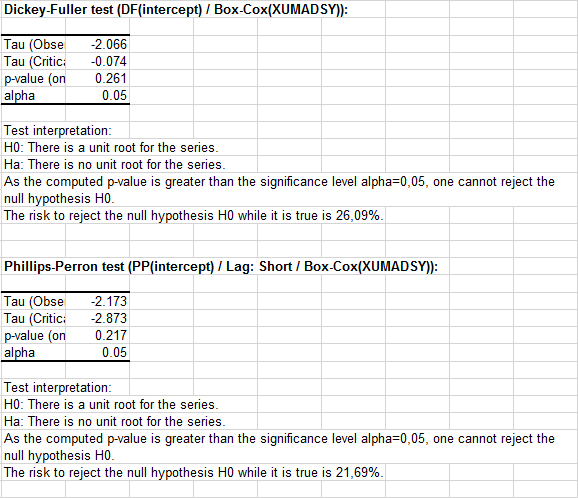
Una vez haya hecho clic en OK, las pruebas se realizan y se muestran los resultados de las dos series.
Para la serie Box-Cox(XUMADSY), ni la prueba DF, ni la prueba PP rechazan la hipótesis nula de una presencia de una raíz unitaria en el proceso de generación de datos (véase siguiente captura de pantalla).

Para la segunda serie, el nivel de confianza que no se debe rechazar la hipótesis nula es aún más fuerte:

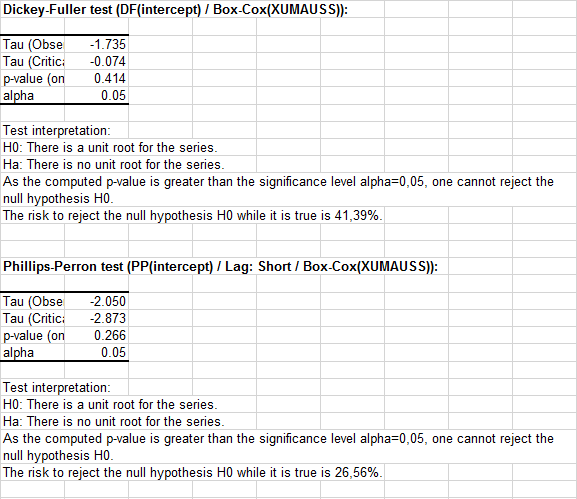
Para concluir con esta parte, parece que el registro de los tipos de cambio a plazo y al contado son ambos I(1). Esto está concuerda con lo que se espera desde la teoría económica.

Ahora deberíamos verificar que existe una relación lineal entre las dos series I(1) que produce una serie I(0).

Configuración de una prueba de cointegración

Para probar la existencia de esta relación, vamos a realizar una prueba de cointegración siguiendo el enfoque de Johansen. Seleccione Análisis de series temporales / Prueba de cointegración:

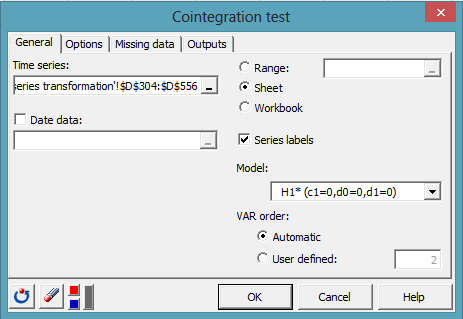
Aparece el cuadro de diálogo de prueba de cointegración como se muestra a continuación. En primer lugar, seleccione las dos series de tiempo transformadas, Box-Cox(XUMADSY) y Box-Cox(XUMAUSS). Seguidamente, debemos seleccionar un modelo para la prueba.

Ambas series tienen medias no-cero sin ninguna deriva y, como se dijo al principio de este tutorial, no se espera que la relación de cointegración tenga una tendencia lineal. Por lo tanto la restricción H1* parece adecuada para nuestra prueba.

Por último, nada sabemos acerca del orden VAR que mejor se adapta a nuestro grupo de series. Vamos a dejar entonces que XLSTAT estime su valor mediante la selección de la opción Automático, como se muestra a continuación.

En la pestaña Opciones, hay que seleccionar un modelo y un criterio para la estimación del orden VAR. Una vez más parece apropiado un modelo con intercepta, y vamos a utilizar el criterio AIC:

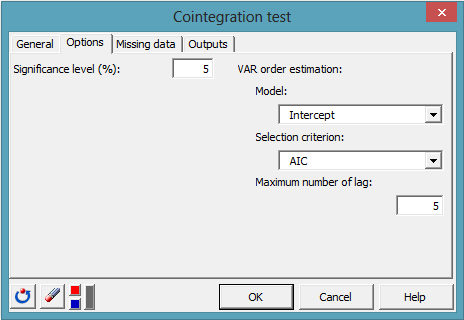
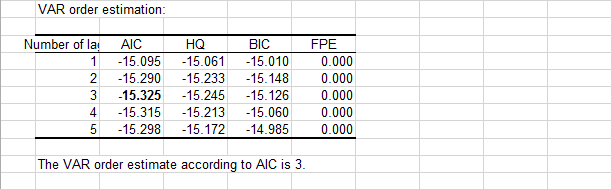
Haga clic en OK y se realizará la prueba de cointegración de Johansen. La primera tabla (véase más adelante) muestra el resultado de la estimación del orden VAR. En negrita, el valor mínimo AIC proporciona un orden VAR de 3 o VAR(3) para nuestro sistema, lo que significa 2 retardos de diferencia para el VECM (Vector Error Correction Model). Podemos comprobar que existe una buena concordancia entre los cuatro criterios.

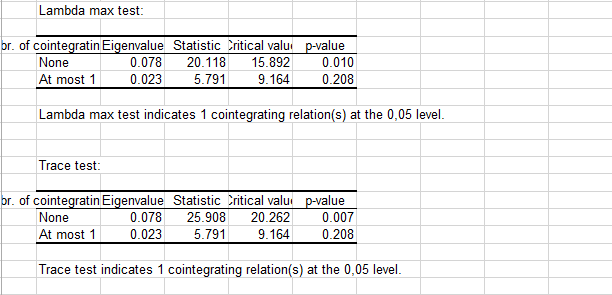
A continuación se muestran los resultados de ambas pruebas, la prueba max eigen (o prueba de lambda) y la prueba trace (véase más adelante). Ambas pruebas concuerdan en el rango(1) de cointegración del sistema o, lo que es equivalente, en la existencia de 1 relación de cointegración entre las dos series. Se estiman los valores p y los valores críticos para ambas pruebas utilizando el método de regresión de superficie descrita en MacKinnon-Haug-Mechelis (1998).

Por último, se proporciona la factorización de la matriz de cointegración en la forma de matriz de impacto (alpha) y los coeficientes de cointegración (beta) siguiendo la normalización propuesta por Johansen:

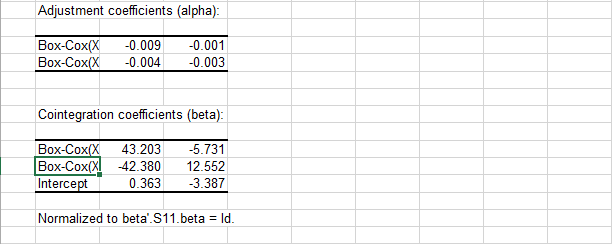
Conclusión

Hemos sido capaces de transformar las dos series de tiempo y realizar pruebas posteriores para validar la hipótesis de dos series I(1).

A continuación, hemos llevado a cabo una prueba de cointegración siguiendo el enfoque de Johansen que nos lleva a la conclusión de que podría existir 1 relación de cointegración entre las dos series.

Por lo tanto, para el período de tiempo de 1979 a 1999, el registro de 12 meses de los tipos de cambio a plazo y al contado de US$ en libras esterlinas muestran una relación de cointegración como se esperaba por la hipótesis de paridad de intereses CIP (Covered Interest Parity). Ahora, usted debe probar su propio análisis utilizando otro conjunto de datos. ¿Qué pasaría con el mismo conjunto de datos, pero hasta la fecha actual? Esto podría llevar a algunos resultados sorprendentes.