Raíz Unitaria (Dickey-Fuller) y estacionalidad en Excel

Este tutorial le mostrará cómo configurar e interpretar pruebas de raíz unitaria y estacionariedad (unit root and stationarity tests) - pruebas de Dickey-Fuller, Phillips-Perron & KPSS - en Excel usando XLSTAT.

¿Qué son las pruebas de raíz unitaria y de estacionariedad?

Se dice que una serie de tiempo Y_t (t = 1,2 ...) es estacionaria (en el sentido débil) si sus propiedades estadísticas (expectativa, varianza, autocorrelación) no varían con el tiempo. El ruido blanco es un ejemplo de una serie de tiempo estacionaria, con el caso, por ejemplo, en que Y_t sigue una distribución normal N(mu, sigma^2) independiente de t. Identificar que una serie no es estacionaria permite estudiar después, de dónde proviene la no estacionariedad. Una serie no estacionaria puede, por ejemplo, ser estacionaria en la diferencia (también denominada integrada de orden 1): Y_t no es estacionaria, pero la diferencia Y_t - Y_{t-1} es estacionaria. Es el caso del paseo aleatorio (random walk). Una serie también puede ser estacionaria en tendencia. Las pruebas de estacionariedad poder comprobar si una serie es estacionaria o no. Hay dos enfoques diferentes: pruebas de estacionariedad como la prueba KPSS que consideran como hipótesis nula H0 que la serie es estacionaria, y pruebas de raíz unitaria, tales como la prueba de Dickey-Fuller y su versión aumentada (prueba de Dickey-Fuller aumentada, ADF), o la prueba de Phillips-Perron (PP), para las cuales la hipótesis nula es por el contrario que la serie posee una raíz unitaria y por lo tanto no es estacionaria. XLSTAT incluye a fecha de hoy 4 pruebas de raíz unitaria: la prueba de Dickey-Fuller, la prueba ADF, la prueba PP y la prueba de estacionariedad KPSS.

Datos

Los datos han sido generados utilizando una muestra normal al azar N(0, 1) de 100 observaciones (serie N), una serie estacionaria construida a partir de esa muestra (serie rho =0.8), una serie autocorrelacionada (rho = 1) y una serie de tiempo explosiva (rho=1.1), y una serie que varía linealmente con el tiempo (N-0.1t).

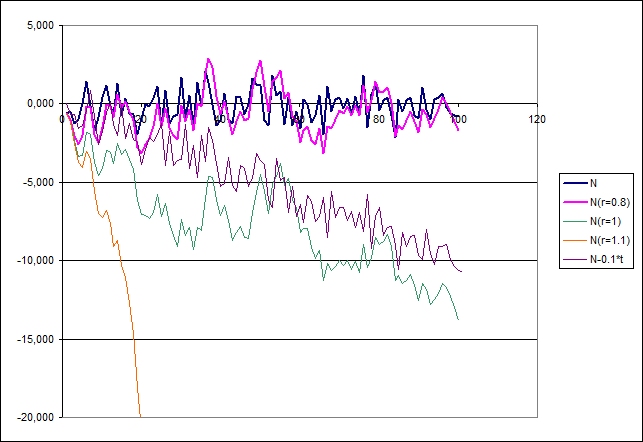Configuración de las pruebas ADF, PP y KPSS sobre una serie de tiempo

Una vez iniciado XLSTAT, elija el comando XLSTAT / Análisis de series temporales / Pruebas de raíz unitaria y estacionariedad.

Una vez haya hecho clic en el botón, aparecerá el cuadro de diálogo. Seleccione los datos en la hoja de cálculo de Excel. En el campo “Series temporales” seleccione la primera y segunda series de tiempo.

Dejamos activada la opción Etiquetas de las series debido a que la primera fila de los datos seleccionados contiene el encabezado de la variable. Seleccionamos la opción ADF(estacionaria) para la prueba aumentada de Dickey-Fuller, ya que la serie no exhibe características explosivas. Elegimos el modelo de intercepción para la prueba PP, ya que parece la más cercana al proceso de generación de los datos de la serie de tiempo. Elegimos la opción de nivel para la prueba KPSS.

En la pestaña Opciones, se puede elegir entre las dos opciones propuestas para estimar los valores de p y los valores críticos para ambas pruebas de raíz unitaria. La opción de regresión superficie utiliza el enfoque propuesto por MacKinnon (J. G. MacKinnon, “Numerical Distribution Functions for Unit Root and Cointegration Tests”, J.A.E., 1996), mientras que la opción Monte Carlo utiliza un número predeterminado de simulaciones. A continuación, se muestran los resultados de la prueba.

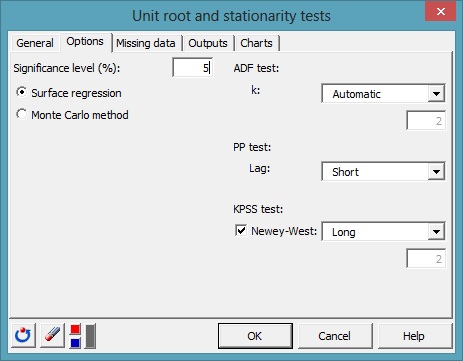
Los cálculos empiezan una vez haya hecho clic en el botón OK.

Interpretación de los resultados de una prueba ADF, una prueba PP y una prueba KPSS (ejemplo sobre serie estacionaria)

Después de los estadísticos de resumen de las dos series seleccionadas, se muestran los resultados de las pruebas ADF, PP y KPSS para la primera, y luego para la segunda serie (ver hoja Dickey-Fuller|Phillips-Perron1).

Podemos ver que las tres pruebas concuerdan para estas series. Para la primera serie, tanto ADF como PP rechazan la hipótesis nula de que la serie sea autocorrelacionada con (r=1) y retiene la hipótesis alternativa de que es estacionaria, y la prueba KPSS mantiene la hipótesis nula de que la serie es estacionaria.

En el caso de la segunda serie, los valores de p no son tan bajos (prueba ADF) o altos (prueba KPSS) como lo fueron con la primera muestra, pero se llega a las mismas conclusiones.

Interpretación de los resultados de una prueba ADF, una prueba PP y una prueba KPSS (ejemplo sobre serie no estacionaria)

A continuación ejecutamos las tres pruebas sobre la columna E, para la cual sabemos a partir de nuestros parámetros de simulación que el proceso de generación tiene una raíz unitaria. Para cada prueba, la raíz unitaria (o no estacionariedad para la prueba KPSS) se detecta con un mayor nivel de significación para la prueba PP (ver resultados en la hoja Dickey-Fuller|Phillips-Perron2).

Para la serie de tiempo en las columnas F (ver resultados en la hoja de Dickey-Fuller|Phillips-Perron3), cambiamos la opción alternativa al explosivo para la prueba ADF y su tendencia para la prueba KPSS. La prueba KPSS conducen a la conclusión de que la serie no es estacionaria, mientras que las dos pruebas de raíz unitaria rechazan la hipótesis de una raíz unitaria en el mecanismo de generación de datos.

Interpretación de los resultados de una prueba ADF una prueba KPSS (ejemplo sobre una serie de tendencia lineal)

Ejecutamos ahora las pruebas sobre la última serie que muestra claramente una tendencia en el tiempo (ver resultados en la hoja Dickey-Fuller|Phillips-Perron4). Hemos seleccionado la opción estacionaria para la prueba ADF, el modelo de intercepción + tendencia para la prueba PP y la versión tendencia para la prueba KPSS. Las tres pruebas concuerdan en que la serie sometida a prueba es estacionaria una vez eliminada la tendencia.