Test de cointégration sur séries temporelles dans Excel

Jeu de données pour réaliser un test de cointégration

Ce tutoriel utilise un jeu de données extrait de la base de données mise à disposition par la banque d'Angleterre (Bank of England). Il est constitué de deux séries temporelles : - La moyenne mensuelle du taux de change à terme 12 mois US$ en Livre Sterling nommée XUMADSY,

• La moyenne mensuelle du taux de change au comptant US$ en Livre Sterling nommées XUMAUSS.

Les deux séries couvrent une période de temps allant de Janvier 1979 à Décembre 1999.

Objectif de ce tutoriel

Les taux d'échange expriment le prix d'une devise étrangère en une autre devise (nationale). Dans ce tutoriel, nous allons considérer le taux de change à terme 12 mois et le taux de change au comptant des dollars américains en livre sterling britanniques sur la période 1979-1999. D'une part, le taux de change à terme 12 mois est un contrat de couverture au sein duquel deux parties se sont entendues au jour J sur la valeur du taux à laquelle ils échangeront les devises dans le futur (ici, 12 mois). D'autre part, le taux de change au comptant traduit la valeur présente du taux entre les deux devises.

Dans le cadre de la parité des taux de change avec couverture, le log des taux de change comptant et à terme sont reliés au différentiel de taux d'intérêt existant entre les deux pays par la relation suivante :

lnForward - lnSpot = rDiff

où lnForward désigne le taux à terme, lnSpot, le taux comptant et rDiff, le différentiel de taux d'intérêt.

Sous l'hypothèse de marché efficaces, une situation dans laquelle une personne peut emprunter dans une devise étrangère, investir à un taux sans risque et verrouiller le prix de change dans la devise nationale via un contrat à terme ne doit pas permettre d'assurer un bénéfice sans risque. En conséquence, le différentiel de taux d'intérêt est attendu comme étant I(0) (ou stationnaire). Par ailleurs, il est généralement admis dans la littérature que les taux de change sont intégrés d'ordre 1 (noté I(1)). Une relation de cointégration doit donc exister entre le log des taux de change à terme et comptant pour qu'une combinaison linéaire de ces deux séries I(1) donne une série I(0).

Dans la suite de ce tutoriel, nous allons tout d'abord transformer nos séries chronologiques et valider leur caractère I(1) au moyen de tests de racine unitaire. Ensuite, nous allons tester si ces deux séries I(1) peuvent effectivement être combinées linéairement pour donner une série I(0). En d'autres termes, nous allons tester le rang de cointégration, ou nombre d'équations cointégrantes, du système via la méthodologie proposée par Johansen.

Transformation des séries chronologiques

Tout d'abord, nous devons transformer les séries extraites de la base de données de la banque d'Angleterre de manière à obtenir leur logarithme. Après avoir ouvert XLSTAT, sélectionnez Time / Transformation de séries temporelles (voir ci-dessous).

La boîte de dialogue Transformation de séries temporelles apparait comme indiqué ci-dessous. Sélectionnez les deux séries temporelles sur la feuille Excel. L'option Libellés des séries doit être activée car la première ligne contient les entêtes des variables.

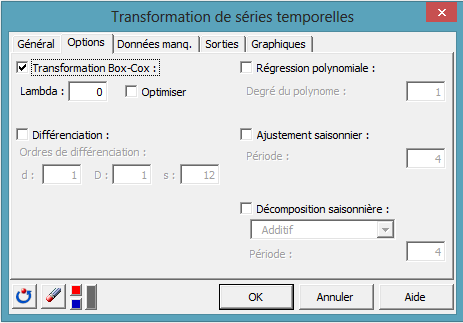
Dans l'onglet Options, sélectionnez Transformation de Box-Cox et saisissez la valeur 0 pour le paramètre Lambda de manière à obtenir le logarithme des séries :

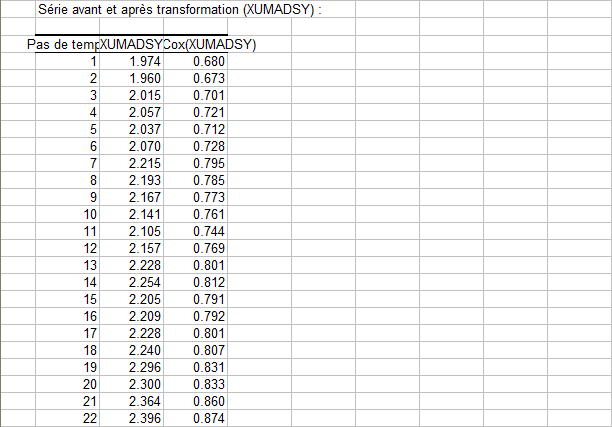
Cliquez sur OK, les calculs sont réalisés et les deux séries transformées sont affichées sur une nouvelle feuille.

Tout d'abord, le taux de change à terme 12 mois (XUMADSY) et sa transformation log (Box-Cox(XUMADSY)) :

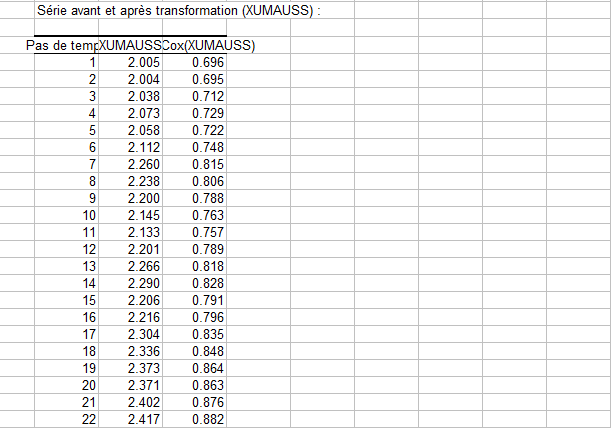
Puis, le taux de change comptant (XUMAUSS) et sa transformation log (Box-Cox(XUMAUSS)) :

Analyse descriptive

Maintenant que nos séries sont prêtes, nous allons leur appliquer une analyse descriptive de manière à vérifier rapidement qu'elles présentent les caractéristiques attendues. Pour réaliser une analyse descriptive, cliquez sur Time / Analyse descriptive comme indiqué ci-dessous.

Sélectionnez les deux séries transformées, Box-Cox(XUMADSY) et Box-Cox(XUMAUSS), en vous aidant de la touche Ctrl pour faire une sélection multiple:

Dans l'onglet Sorties, assurez-vous que les options Autocorrélations et Autocorrélations partielles sont activées comme indiqué ci-dessous : Dans l'onglet Graphiques, activez les options Autocorrélogramme (ACF) et Autocorrélogramme partiel (PACF) :

Une fois que vous avez cliqué sur OK, les descriptions statistiques, ACF et PACF sont affichées pour les deux séries.

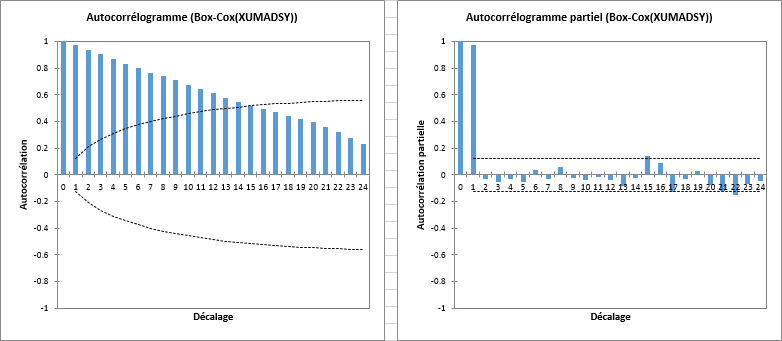
Tout d'abord, comme indiqué ci-dessous, l'ACF de Box-Cox(XUMADSY) indique un large nombre de décalages significatifs.

En regardant la PACF, le décalage 1 semble le seul réellement significatif. Il semble que les hauts niveaux de corrélations de l'ACF soient largement expliqués par le décalage 1.

Ce comportement est tout à fait compatible avec ce qui est attendu pour un processus générateur I(1).

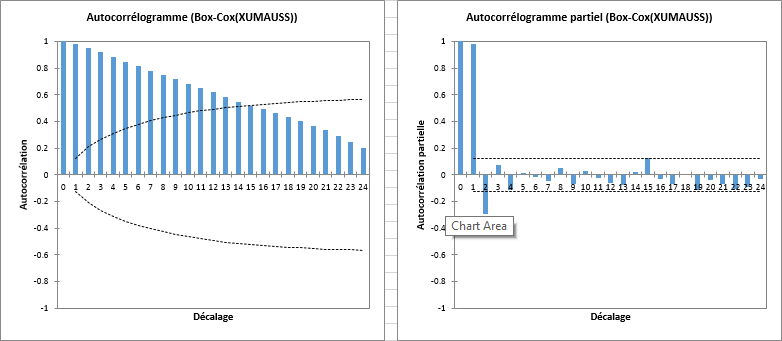
La situation est similaire pour la seconde série temporelle Box-Cox(XUMAUSS) avec un décalage 1 fortement significatif:

Tests de racine unitaire

Après ces vérifications préliminaires, nous sommes prêts pour tester le caractère intégré d'ordre 1 de nos séries transformées. Pour ce faire, nous réaliserons des tests de racine unitaire sur chacune de nos séries : un test de Dickey-Fuller (DF) et un test de Phillips-Perron (PP). SélectionnezTime / Tests de racine unitaire et de stationnarité.

Dans le champ Séries temporelles, sélectionnez les deux séries transformées, Box-Cox(XUMADSY) et Box-Cox(XUMAUSS), puis activez les tests de Dickey-Fuller et Phillips-Perron comme indiqué ci-dessous :

Concernant le choix du modèle, celui avec une constante est le plus approprié pour nos données. Il faut donc sélectionner ce modèle pour les deux tests DF et PP.

Cliquez sur OK pour lancer l'exécution des tests. Les résultats sont affichés successivement pour les deux séries.

Pour la série Box-Cox(XUMADSY), aucun des deux tests ne parvient à rejeter l'hypothèse nulle de présence d'une racine unitaire dans le processus générateur (voir ci-dessous).

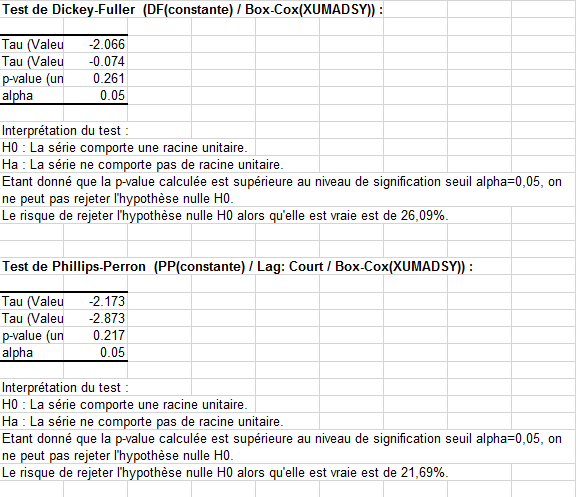Pour la seconde série, la p-value est encore plus élevée :

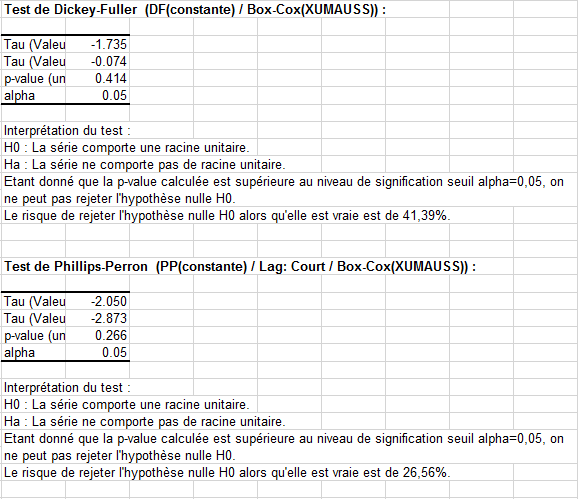Pour conclure sur cette partie, il semble que les logarithmes des taux de change à terme et comptant soient effectivement I(1). Ceci est en accord avec le consensus que l'on trouve dans la littérature financière.

Nous allons maintenant chercher à déterminer si une combinaison linéaire de ces deux séries I(1) peut permettre d'obtenir une série I(0).

Paramétrer un test de cointégration

Afin de tester l'existence de cette relation linéaire, nous allons réaliser un test de cointégration en suivant l'approche proposée par Johansen. Cliquez surTime / Test de cointégration :

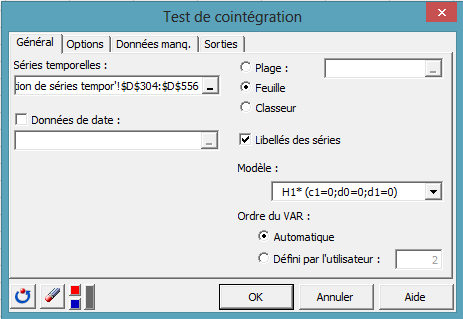
La boîte de dialogue du test de cointégration apparait comme indiqué ci-dessous. Tout d'abord, sélectionnez les séries transformées, Box-Cox(XUMADSY) and Box-Cox(XUMAUSS).

Puis sélectionnez un modèle pour le test. Les deux séries transformées présentent une moyenne non nulle sans tendance et la relation de cointégration attendue dans le cadre de la parité des taux de change avec couverture ne doit pas présenter de tendance. Le modèle H1* semble donc appliquer les restrictions qui conviennent le mieux à notre test.

Enfin, nous ne connaissons pas l'ordre du VAR qui décrit le mieux notre groupe de séries. Nous allons donc laisser XLSTAT l'estimer automatiquement en activant l'option Automatique comme indiqué ci-dessous.

Dans l'onglet Options, sélectionnez le modèle et un critère de sélection pour l'estimation de l'ordre du VAR. Un modèle avec Constante semble approprié et nous utiliserons le critère AIC :

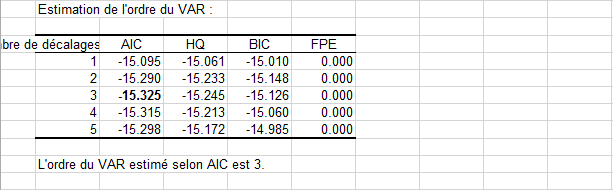
Cliquez sur OK et le test de cointégration selon Johansen est lancé. Le premier tableau (voir ci-dessous) affiche les résultats obtenus pour l'estimation de l'ordre du VAR. En gras, le critère AIC est minimum pour un ordre de VAR de 3, noté VAR(3), pour notre système. Ceci signifie 2 décalages dans la représentation VECM (modèle vecteur à correction d'erreur). Nous pouvons vérifier que l'ordre estimé est cohérent entre les différents critères. 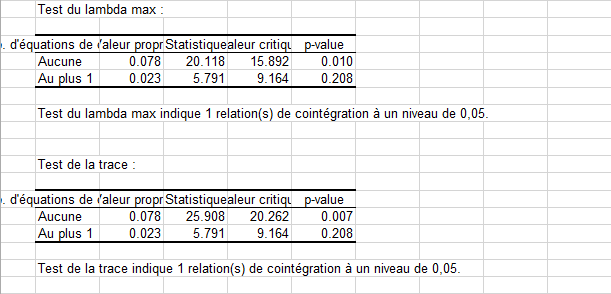Ensuite, les résultats des deux tests réalisés, le test du lambda max ainsi que le test de la trace sont indiqués (voir ci-dessous). Les deux tests sont en accord sur le rang(1) de cointégration du système ou, de manière équivalente, sur l'existence d'une relation de cointégration entre les deux séries temporelles. Les p-values et valeurs critiques sont estimées via la régression surfacique décrite dans MacKinnon-Haug-Mechelis(1998).

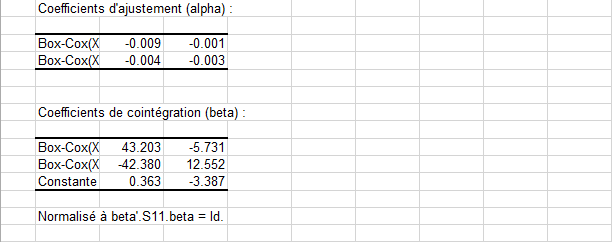
Enfin, la factorisation de la matrice cointégrante est donnée sous la forme de la matrice d'impact (alpha) et des coefficients cointégrants (beta) selon la normalisation proposées par Johansen :

Conclusion

Nous avons pu transformer les deux séries temporelles et réaliser sur celles-ci des tests pour valider l'hypothèse de deux séries I(1).

Ensuite, nous avons réalisé un test de cointégration selon la méthodologie proposée par Johansen qui nous a conduit à conclure qu'une équation de cointégration existe entre les deux séries.

Ainsi, pour la période allant de 1979 à 1999, les taux de change à terme et comptant du dollar américain en livre sterling britannique présentent une relation de cointégration comme attendu sous l'hypothèse de parité des taux de change avec couverture. Maintenant, vous pouvez essayer de mener votre propre analyse avec un autre jeu de données. Pourquoi ne pas essayer le même jeu de données mais en l'étendant jusqu'à aujourd'hui? Vous obtiendrez peut-être des résultats étonnants.