Régression non linéaire dans Excel
Ce tutoriel explique comment mettre en place et interpréter une régression non linéaire dans Excel avec XLSTAT.
Jeu de données pour réaliser une régression non linéaire et but de ce tutoriel
La régression non linéaire permet de modéliser des phénomènes complexes n'entrant pas dans le cadre du modèle linéaire.
Les données sont fictives et ont été créées pour ce tutoriel.
En utilisant la régression non linéaire, notre but est d'étudier la relation entre la concentration en substrat d’une enzyme et sa vitesse maximale dans dans deux groupes différents. Pour ce faire, nous utiliserons le modèle de Michaelis-Menten.
Paramétrer une régression non linéaire
Une fois XLSTAT lancé, cliquez sur le menu XLSTAT / Modélisation / Régression non linéaire.
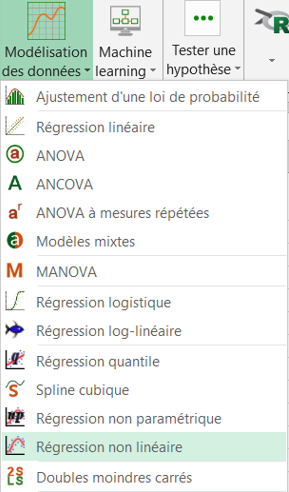
La boîte de dialogue correspondant à la régression non linéaire apparaît, vous pouvez alors sélectionner les données sur la feuille Excel.
La Variable dépendante correspond à la variable réponse (ou variable à modéliser), qui est dans ce cas précis la "Vitesse".
La variable quantitative explicative est la concentration en substrat : conc.
On veut expliquer la variabilité de la Vitesse par celle de la concentration en substrat conc.
La variable groupe permet de séparer les données pour chacun des groupes a et b. L'option Libellés des variables est laissée activée car la première ligne des colonnes comprend le nom des variables.
Dans l'onglet Fonctions, XLSTAT propose un choix large de fonctions prédéfinies dont les dérivées sont directement prisent en compte.
NB : XLSTAT laisse aussi le choix à l’utilisateur de rentrer une fonction définie par lui-même. L’utilisateur aura alors le choix de rentrer ses propres dérivées, ou de les laisser estimé par XLSTAT.

Une fois que vous avez cliqué sur le bouton OK, les calculs commencent puis les résultats sont affichés.
Interprétation des résultats de la régression non linéaire
Le premier tableau de résultats fournit des statistiques simples sur les données sélectionnées. Le second tableau (ci-dessous) donne les coefficients d'ajustement du modèle parmi lesquels le RMCE (racine de la moyenne des carrés des erreurs) qui donne une idée de la qualité d'un modèle. Un modèle ajustant mieux les données qu’un autre aura une RMCE plus faible. La somme des carrés des résidus (SCE) est le critère utilisé par XLSTAT pour ajuster le modèle.
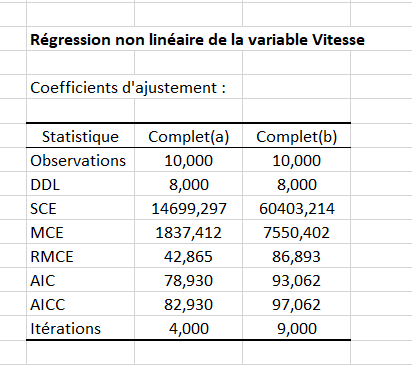
Dans notre cas, la RMCE est 42,865 dans le 1er groupe, et 86.893 dans le second, ce qui montre que la variabilité de la vitesse est mieux expliquée dans le 1er groupe.
Le tableau suivant fournit les détails sur les paramètres du modèle après ajustement pour chacun des groupes. Nous voyons que les paramètres pr1, qui correspondent à la vitesse maximale du groupe a et du groupe b, sont assez proches.

Les équations des modèles ajustés sont fournies. La syntaxe est compatible avec Excel afin de rendre sa réutilisation aisée.

Le tableau suivant (voir feuille Excel) présente l'analyse des résidus. On remarque que les observations pour lesquelles le modèle est le moins bien ajusté sont les deux premières observations de chacun des groupes.
Le premier graphique (voir ci-dessous) permet de visualiser les données et les courbes des modèles ajustés, et confirme que la vitesse maximale de chacun des groupes est proche. Les autres graphiques permettent d'analyser les résidus, et sont particulièrement utiles lorsque le nombre de données est important.

Comme on a pu le voir auparavant, la vitesse maximale des deux groupes est très proche. Vous pouvez donc partager ce paramètre afin d’obtenir une valeur d’ajustement globale pour celui-ci.
Pour cela, relancez une analyse. Dans l’onglet options cochez « paramètres partagés » puis cliquez sur OK.

Une nouvelle fenêtre va apparaitre, dans laquelle vous choisissez de partager le paramètre « pr1 », correspondant à la vitesse maximale.

Vous pouvez maintenant voir, dans le tableau des paramètres du modèle, que les paramètres « pr1 » ont la même valeur pour les deux groupes.


Ceci nous permet d’avoir un modèle avec une vitesse globale entre les groupes.
En conclusion, dans le cadre de cette étude et du modèle choisi, la concentration en substrat permet de modéliser très efficacement sa vitesse.
Cet article vous a t-il été utile ?
- Oui
- Non