Kolmogorov-Smirnov Test in Excel - Anleitung

Dieses Tutorium zeigt Ihnen, wie Sie einen Kolmogorov-Smirnov Test zum Vergleichen von zwei Verteilungen in Excel mithilfe von XLSTAT ausführen und interpretieren. Sie sind sich nicht sicher, ob dies der statistische Test ist, nach dem Sie suchen? Weitere Hinweise finden Sie hier.

Datensatz für einen Kolmogorow-Smirnow-Test zum Vergleich zweier Verteilungen

Sie können

Ziel dieses Tutorials

Dieses Tutorial setzt sich aus zwei Teilen zusammen:

Im ersten Teil werden die Verteilungen der beiden Stichproben ohne Annahmen hinsichtlich zugrundeliegender theoretischer Verteilungen (z. B. Normalverteilung) verglichen. Verwendet wird der für diesen Fall sehr gut geeignete nichtparametrische Kolmogorow-Smirnow-Test.

Im zweiten Teil wird im Kolmogorow-Smirnow-Test die Verteilung einer Stichprobe mit einer theoretischen Verteilung verglichen.

Teil 1: Ausführen eines Kolmogorow-Smirnow-Tests zum Vergleich zweier beobachteter Verteilungen

Zunächst werden die Verteilungen der beiden Stichproben verglichen.

Sehen wir uns hierzu die Verteilungen selbst an. Für die Visualisierung stetiger Verteilungen eignen sich Histogramme: XLSTAT / Visualisierung der Daten / Histogramme. Wählen Sie auf der Registerkarte Allgemein die Datenzellen beider Stichproben aus. Aktivieren Sie auf der Registerkarte Optionen die kleinste Option, und geben Sie "0" in das Feld ein. Auf diese Weise wird die X-Achse zur unteren Grenze beider Histogramme, was den Vergleich erleichtert. Klicken Sie auf die Schaltfläche "OK".

Die Histogramme werden in der Ergebnistabelle angezeigt:

Ohne jegliche theoretische Annahmen können wir feststellen, dass die Verteilung von Stichprobe B im Vergleich zu der von Stichprobe A zu niedrigen Werten tendiert. Nun vergleichen wir die beiden Verteilungen mithilfe des nichtparametrischen Kolmogorow-Smirnow-Tests: XLSTAT / Nichtparametrische Tests / Vergleich zweier Verteilungen**.

Wählen Sie unter "Stichprobe 1" (Sample 1) die Spalte mit Marke A aus und unter "Stichprobe 2" (Sample 2) die Spalte mit Marke B. Im Kolmogorow-Smirnow-Test sind unausgeglichene Stichproben wie die unserer Beispieldaten zulässig: Stichprobe B enthält weniger Werte als Stichprobe A. Beachten Sie, dass Sie auf der Registerkarte Optionen eine einseitige Alternativhypothese und/oder eine exakte Berechnung des p-Werts (p-value) auswählen können. Aktivieren Sie auf der Registerkarte Diagramme die Option "Kumulative Histogramme". Klicken Sie auf die Schaltfläche "OK".

In der Ergebnistabelle wird die Kolmogorow-Smirnow-Statistik (0,475) aufgeführt, die leicht extrahiert werden kann (siehe dazu das Diagramm für kumulative Histogramme). Diese Statistik enthält einen p-Wert (p-value) von 0,133, der darauf hinweist, dass sich die beiden Verteilungen mit einem alpha-Wert von 0,05 nicht signifikant unterscheiden.

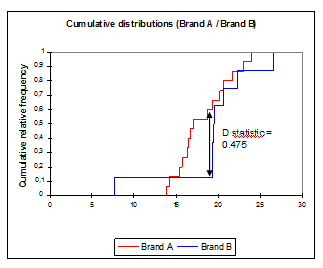
Im Diagramm der kumulativen Verteilungen ist die betrachtete Variable (Umfragewerte) auf der X-Achse dargestellt. Für einen gegebenen Punkt auf der X-Achse ergibt sich die kumulative relative Häufigkeit einer Marke aus dem Verhältnis zwischen den Werten unterhalb dieses Punkts und den gesamten Werten der Marke. Wie zuvor in den Histogrammen angedeutet, beginnt die Kumulation der Werte von Marke B früher als die von Marke A auf der X-Achse. Sehen wir uns nun die Mittelwerte an, also die Werte, die einer relativen Summenhäufigkeit von 0,5 entsprechen. Der Mittelwert für Marke B (~20) scheint höher zu sein als der für Marke A (~17).

Bei der D-Statistik des Kolmogorow-Smirnow-Tests handelt es sich um die höchste Abweichung zwischen den beiden Kurven. In diesem Beispiel liegt die Abweichung im mittleren Bereich, jedoch muss dies nicht unbedingt für andere Daten gelten. Je höher die D-Statistik ausfällt, desto niedriger liegt der p-Wert und desto signifikanter ist der Unterschied zwischen den beiden Verteilungen.

Teil 2: Ausführen eines Kolmogorow-Smirnow-Tests zum Vergleich einer beobachteten und einer theoretischen Verteilung

Angenommen, die Qualitätswerte von Marke A wären in Frankreich erhoben worden. Für Kunden aus den USA entspricht dieser Wert einer Normalverteilung mit einem Mittelwert von 21,5 und einer Standardabweichung von 2,3. Nun stellt sich die Frage, ob sich die Verteilung der französischen Werte signifikant von der theoretischen Verteilung der Werte aus den USA unterscheidet. Erneut kommt der Kolmogorow-Smirnow-Test zum Einsatz. Der Unterschied zum vorherigen Teil besteht darin, dass anstelle eines Vergleichs zweier unterschiedlicher Verteilungen nun eine beobachtete Verteilung mit einer theoretischen verglichen wird.

XLSTAT / Nichtparametrische Tests / Anpassung einer Verteilung. Wählen Sie auf der Registerkarte **Allgemein die Daten von Marke A und die Normalverteilung aus. Aktivieren Sie dann die Option Eintragen, und geben Sie die folgenden Parameter ein: µ = 21,5 und Sigma = 2,3. Aktivieren Sie auf der Registerkarte "Diagramme" die Option "Kumulative Histogramme". Klicken Sie auf die Schaltfläche "OK".

Das Histogramm (unten links) in der Ergebnistabelle deutet darauf hin, dass die beobachtete Verteilung im Vergleich zu der theoretischen Kurve mit der Verteilung der Werte aus den USA (rote Linie) auf niedrigen Werten beruht.

Der Kolmogorow-Smirnow-Test mit einem p-Wert von 0,000 führt zu dem Ergebnis, dass sich die beobachtete Verteilung signifikant von der theoretischen Verteilung mit einem alpha-Wert von 0,05 unterscheidet.