How to interpret contradictory results between ANOVA and multiple pairwise comparisons?
This article explains how to interpret contradictory results between ANOVA and multiple pairwise comparisons, also referred as post hoc comparisons.
A few words on multiple comparisons tools
Why do we need to use multiple pairwise comparisons tests?
The aim of ANOVA is to detect whether a factor has a significant effect on a dependent variable globally. For example, we may study how smoking affects pulmonary health. Smoking is the factor involving 4 population groups (non-smokers, passive smokers, light smokers and heavy smokers).
Assuming that ANOVA detects a significant effect of smoking on the pulmonary health, we can go a step further and examine whether specific population groups differ significantly from one another. For this purpose, we need to test the differences between all pairs of groups. Pairwise multiple comparisons tests, also called post hoc tests, are the right tools to address this issue.
What is the multiple comparisons problem?
Pairwise multiple comparisons tests involve the computation of a p-value for each pair of the compared group. The p-value represents the risk of stating that an effect is statistically significant while this is not true. As the number of pairwise comparisons increases, and therefore the number of p-values, it becomes more likely to detect significant effects which are due to chance in reality. For example, given a significance level alpha of 5%, we would likely find 5 significant p-values by chance over 100 significant p-values.
To deal with this problem, multiple pairwise comparisons tests involve p-value corrections: p-values are penalized (= their value is increased) as the number of comparisons increase. Therefore, it becomes less likely to draw erroneous inferences. Note that the p-value penalization procedure differs from one post hoc test to another.
To find out how to run an ANOVA followed by multiple comparisons in Excel using XLSTAT, check out the tutorial here.
Interpretation of contradictory results between ANOVA and multiple pairwise comparisons
As explained in the above session, ANOVA and multiple pairwise comparison tests examine different questions. The computations made to provide the answers rely on different methodologies. It is therefore possible that the results generated are contradictory in some cases.
Significant ANOVA with non-significant multiple pairwise comparisons
This conclusion can be drawn when:
- The p-value computed by the ANOVA is less than or equal to the alpha significance level (e.g. 0,05).
- All the p-values computed by the multiple pairwise comparisons test are higher than the alpha significance level.
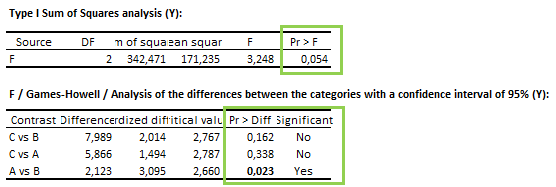
An example is displayed below:

Here are some suggestions why post-hoc tests may appear non-significant while the global effect is significant. The list below is not exhaustive. Other situations exist.
- A lack of statistical power. For example, when groups have small sizes. When pairwise comparison tests are not statistically powerful, it is less likely to detect significant differences.
- A high number of factor levels can also be an explanation. The more the pairwise comparisons, the more the p-values get penalized. Thus the risk of rejecting null hypotheses while this is true decreases.
- A weakly significant global effect (p-value of the ANOVA table is equal or close to the significant level).
- A conservative multiple comparisons test. The more conservative the test, the more likely to reject significant differences between means that in reality are meaningful.
Non-significant ANOVA with significant multiple pairwise comparisons
This conclusion can be drawn when:
- The p-value computed by the ANOVA is higher than the alpha significance level (e.g. 0,05).
- At least one p-value computed by the multiple pairwise comparisons test is lower than the alpha significance level.
An example is displayed below:
An unfortunate common practice is to pursue multiple comparisons only when the hull hypothesis of homogeneity is rejected. (Hsu, page 177).
In some cases, post-hoc tests can be powerful enough to find significant differences between group means even if the global effect is not significant. Generally, we can consider such results as valid with one exception (protected Fisher LDS).
War dieser Artikel nützlich?
- Ja
- Nein