Análisis Discriminante: tutorial en Excel

Este tutorial muestra cómo configurar e interpretar un Análisis discriminante (DA) en Excel usando el software XLSTAT.

Datos para ejecutar un análisis discriminante

Los datos proceden de [Fisher M. (1936). The Use of Multiple Measurements in Taxonomic Problems. Annals of Eugenics, 7, pp 179 -188] y corresponden a 150 flores de la familia Iris, definidas por 4 variables cuantitativas (Longitud-Sépalos, Anchura-Sépalos, Longitud-Pétalos, Anchura-Pétalos) y por su especie. Tres diferentes especies forman parte de este estudio: setosa, versicolor and virginica.

Objetivo de este análisis discriminante

Nuestro objetivo es probar si las cuatros variables descriptivas permiten identificar las especies, y visualizar los datos en un gráfico con el fin de comprobar que las tres especies son correctamente diferenciadas

Iris setosa, versicolor et virginica.

Configuración de un análisis discriminante

• Una vez XLSTAT iniciado, elija el comando XLSTAT / Análisis de los datos / Análisis Factorial Discriminante.

• Una vez el botón presionado, aparece el cuadro de diálogo correspondiente al análisis Factorial Discriminante (AFD).

• Puede entonces seleccionar los datos en la hoja Excel. La "Variable dependiente" corresponde a la variable explicada, que es, en este caso preciso, la especie de Iris.

• Las variables explicativas son las cuatros variables que disponemos.

• Se deja la opción "Etiquetas de las columnas" activada ya que la primera fila de las columnas incluye el nombre de las variables.

• En la pestaña Opciones, desmarcamos la opción Igualdad de matrices de covarianza porque, como veremos con la prueba de Box, asumir que las matrices de covarianza de las tres especies son iguales sería incorrecto.

• Para evitar añadir demasiada información en los gráficos, hemos desmarcado la opción Etiquetas en la pestaña Gráficos.

• Los cálculos comienzan una vez que haga clic en OK. Los resultados se mostrarán a continuación.

Interpretación de los resultados de un análisis discriminante

Una vez que haya pulsado en el botón OK, empiezan los cálculos y luego se visualizan los resultados. XLSTAT empieza por visualizar las matrices implicadas en los cálculos. Las dos pruebas de Box permiten confirmar que no se puede efectuar la hipótesis que las matrices de covarianza son idénticas para las 3 especies.

La prueba del Lambda de Wilks permite probar si los vectores de las medias para los diferentes grupos son iguales o no (esta prueba se puede percibir como un equivalente multidimensional de la prueba LSD de Fisher o de la prueba HSD de Tukey). Aquà­ observamos que la diferencia entre los vectores es significativa al nivel de significación de 0.05.

La siguiente tabla proporciona los valores propios y el % de varianza correspondiente. Se puede ver que 99% de la varianza están representadas por el primer factor. Hay nada más que dos factores: en efecto, el número máximo de factores no nulos vale k-1, cuando n>p>k, donde n es el número de observaciones, p el número de variables explicativas y k el número de grupos.

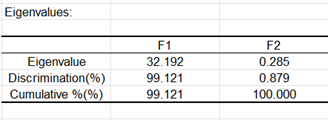
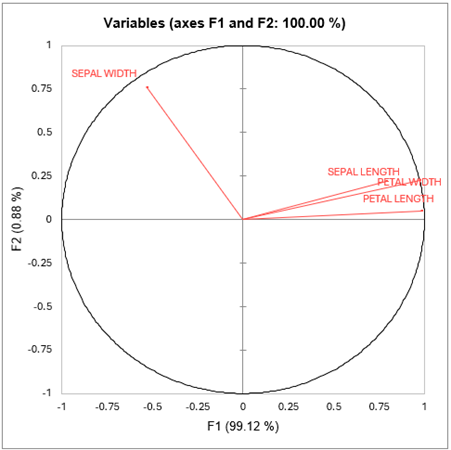
El siguiente gráfico muestra como las cuatro primeras variables están correladas con los dos factores obtenidos (este gráfico está construido a partir de la tabla de las coordenadas de las variables). Se puede observar que el factor F1 está correlado con Long. Sép., Long. Pét. et Anch. Pét. y que F2 está correlado con Anch. Pét.

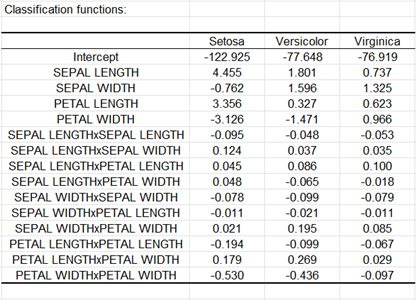
En la siguiente tabla se visualizan las funciones discriminantes. Cuando se supone que las matrices de covarianza son iguales, estas funciones son lineales. En el caso contrario, son cuadráticas, como es el caso aquà­. La regla basada sobre estas funciones es tal que se le atribuye una observación al grupo cuya función discriminante da el valor más elevado.

La siguiente tabla enumera para cada flor, sus coordenadas factoriales, la probabilidad de asignación a cada grupo, y el cuadrado de las distancias de Mahalanobis en el centroide de cada grupo. Cada observación es reclasificada en el grupo por el cual la probabilidad es máxima. Las probabilidades son probabilidades a posteriori que toman en cuenta las probabilidades a priori a través de la fórmula de Bayes.

Se nota que las observaciones (5,9,12) fueron reclasificadas. Puede haber varias razones: la persona que efectuó mis mediciones ha cometido un error cuando medà­a, o los iris que corresponden a estos datos han tenido un crecimiento anormal por razones desconocidas, o el criterio de clasificación utilizado por el especialista no es correcto, o falta de información para diferenciar perfectamente las especies entre sà­.

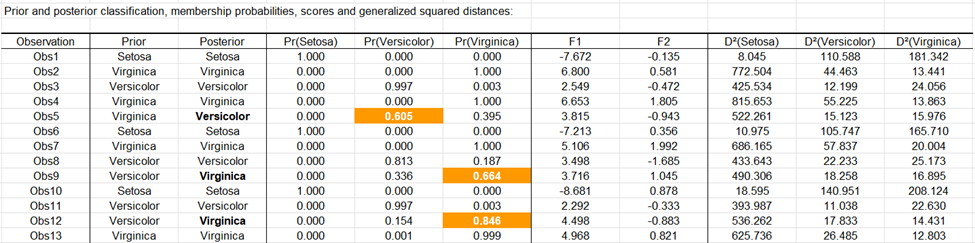
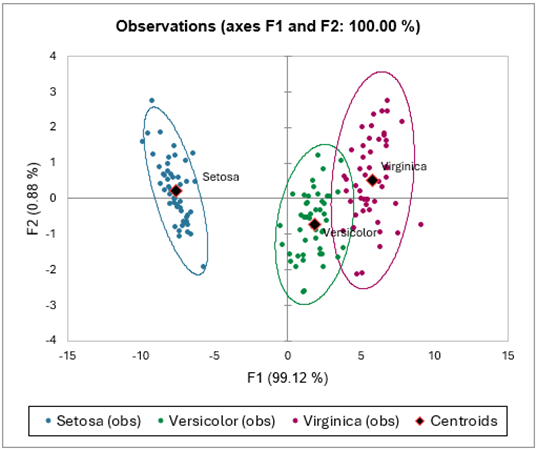
En el siguiente gráfico representa las observaciones sobre los ejes factoriales. Este gráfico permite confirmar que las observaciones están correctamente discriminados sobre los ejes factoriales obtenidos a partir de las variables explicativas iniciales.

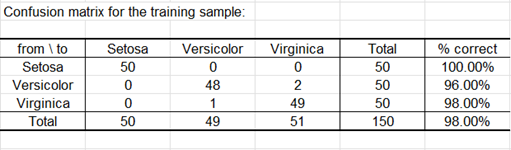
Por último, la matriz de confusión resume la información que concierne las reclasificaciones de observaciones, y se puede deducir el à­ndice de error aparente, que corresponde a la razón del número de observaciones reclasificadas, sobre el número total de observaciones.

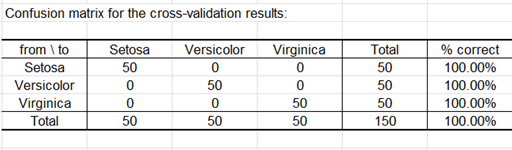
Dado que se ha activado la opción correspondiente en la pestaña "Resultados" del cuadro de diálogo, se calculan las predicciones para la validación cruzada. La validación cruzada permite ver cuál sería la predicción para una observación dada si se excluye de la muestra de estimación. Podemos ver aquí que sólo una observación más (Obs5) está mal clasificada.

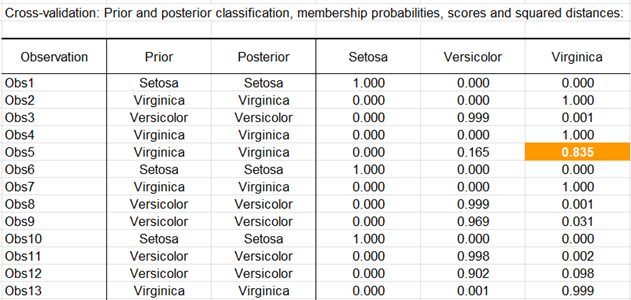
La matriz de confusión de la validación cruzada se muestra a continuación.