Test de Cochran-Mantel-Haenszel dans Excel

Ce tutoriel explique comment calculer et interpréter un test non-paramétrique de Cochran-Mantel-Haenszel avec Excel en utilisant XLSTAT.

Jeu de données pour réaliser un test de Cochran-Mantel-Haenszel dans Excel avec XLSTAT

Les données proviennent de [Mantel N. (1963). Chi-Square Tests with One Degree of Freedom; Extensions of the Mantel- Haenszel Procedure. Journal of the American Statistical Association, 58, 303, 690-700.] et correspondent à une expérience pendant laquelle on injecte à des lapins des streptocoques beta-hémolytiques, puis immédiatement ou 90 minutes plus tard une dose plus ou moins importante de pénicilline.

Le but de l'expérience est de vérifier dans un premier temps s'il existe une dépendance entre la survie ou le décès du lapin et le délai d'injection de la pénicilline.

Paramétrer un test de Cochran-Mantel-Haenszel

Une fois XLSTAT lancé, cliquez sur l’icône Tests non paramétriques et choisissez la fonction Tests de Cochran-Mantel-Haenszel.

Une fois le bouton cliqué, la boîte de dialogue apparaît. Vous pouvez alors sélectionner les données sur la feuille Excel.

Deux formats sont possibles. A titre illustratif les deux formats de données sont présentés dans la feuille de données. Cependant, pour le tutoriel, seul le format Tableaux de contingence est utilisé.

Vous devez sélectionner dans un premier temps les 5 tableaux de contingence (chacun correspondant à un niveau de pénicilline).

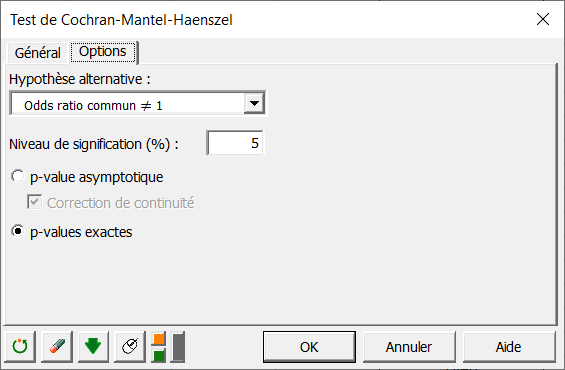
L'option Libellé des colonnes est laissée activée car la première ligne de la sélection comprend le nom des deux modalités de la variable réponse (Survie ou Décès). Dans les options, l’hypothèse alternative proposée n'est valable que lorsque les tableaux sélectionnés sont de format 2x2, ce qui est le cas ici.

L'option Odds ratio commun <> 1 correspond à l'hypothèse alternative de dépendance.

Dans le cas des tableaux 2x2 il est possible de calculer une p-value exacte. Une fois que vous avez cliqué sur le bouton OK, les calculs sont effectués, puis les résultats sont affichés.

Interpréter les résultats d'un test de Cochran-Mantel-Haenszel

XLSTAT fournit d'abord un tableau dans lequel sont consignés les V de Cramer, la statistique du Khi² et la p-value (exacte dans le cas de tableaux 2x2) permettant d'évaluer pour chaque sous-tableau s'il correspond à un cas d'indépendance ou non. Ces statistiques ne sont calculables que si les sommes marginales sont non nulles dans chacun des sous-tableaux. Nous voyons ici que seul le tableau correspondant à la dose 1/2 est proche de la dépendance.

Le V de Cramer présente l'intérêt d'être interprétable en terme de force de lien entre les variables. Dans le cas de tableaux 2x2, il est en effet proche de 0 lorsqu'il n'y a pas de lien, de -1 lorsque les modalités croisées (1 et 2, 2 et 1) sont liées, et proche de 1 lorsque les modalités de même indice (1 et 1, 2 et 2) sont liées.

Néanmoins, lorsque l'on prend les tableaux dans leur ensemble pour un test de Cochran-Mantel-Haenszel, on obtient un Odds ratio commun de 0.143, avec un intervalle de confiance à 95% ne comprenant pas la valeur 1, et une p-value exacte de 0.04 (on obtient 0.047 dans le cas non exact), ce qui amène à conclure qu'il y a globalement un lien entre le délai et le fait qu'un lapin survive ou non à l'injection des streptocoques.

Ce résultat peut paraître surprenant car aucun des sous-tableaux pour lesquels on pouvait calculer les statistiques ne montrait une dépendance. En cumulant les tableaux on arrive cependant à faire ressortir cette dépendance. L'Odds ratio étant différent de 1, on a donc un effet positif sur la survie d'une injection sans délai de pénicilline.

Le test de Cochran-Mantel-Haenszel est à utiliser avec précaution. Il est notamment déconseillé de l'utiliser lorsque l'on a une interaction de niveau 3 entre les 3 variables utilisées. Dans notre cas, cela correspondrait à la situation où plus la dose de pénicilline serait élevée, plus cela augmenterait l'impact du délai. Cela peut se traduire par une évolution du V de Cramer passant une valeur proche de -1 à 1. Et malgré une forte dépendance évidente, le test de Cochran-Mantel-Haenszel pourrait conclure à l'indépendance. D'où l'intérêt que les V de Cramer soient à peu près homogène si l'on conclut à l'indépendance.