Classification Ascendante Hiérarchique CAH dans Excel
Ce tutoriel vous aidera à configurer et interpréter une Classification Ascendante Hiérarchique (CAH) dans Excel avec le logiciel XLSTAT.
Jeu de données sur la Classification Ascendante Hiérarchique
Les données proviennent du US Census Bureau. Elles correspondent à la mesure de paramètres démographiques dans 51 États des Etats-Unis en 2000 et 2001. Dans le cadre de ce tutoriel, seules les données de l'année 2001 ont été conservées et, afin de supprimer les effets d'échelle, les variables initiales ont été converties en taux pour 1000 habitants.
But de ce tutoriel sur la Classification Ascendante Hiérarchique
Le but est ici de créer des groupes homogènes d'Etats. Ces données sont aussi utilisées pour le tutoriel de l'Analyse en Composantes Principales (ACP) et de la classification k-means.
Paramétrer une Classification Ascendante Hiérarchique
-
Une fois que XLSTAT est activé, cliquez sur Analyse de données / Classification Ascendante Hiérarchique (CAH) dans le menu XLSTAT.
-
Une fois le bouton cliqué, la boîte de dialogue correspondant à la Classifciation Ascendante Hiérarchique apparaît. Vous pouvez alors sélectionner les données sur la feuille Excel.
Note : Il y a plusieurs façons de sélectionner les données dans la boîte de dialogue XLSTAT (voir le tutoriel sur le sujet : Sélectionner les données dans Excel avec XLSTAT).
-
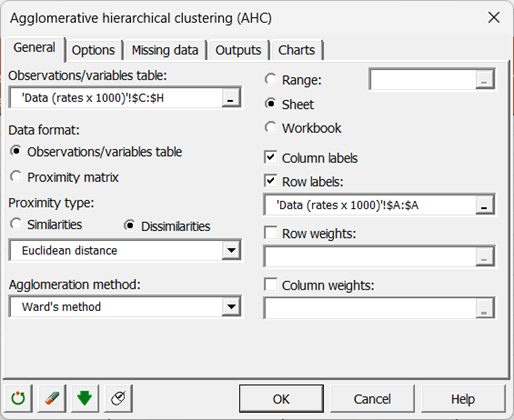
Dans l'exemple étudié ici, les données commencent dès la première ligne, il est donc plus rapide de choisir le mode de sélection par colonnes. C'est pourquoi dans la boîte de dialogue ci-dessous les sélections apparaissent sous forme de colonnes.
-
La variable "Population totale" n'a pas été sélectionnée car seuls les aspects dynamiques de la population nous intéressent ici. La dernière colonne n'a pas non plus été sélectionnée, car nous avons vu avec l'analyse en composantes principales que les deux dernières colonnes sont parfaitement corrélées.
-
L'option Libellés des colonnes est laissée activée, car la première ligne de données contient le nom des variables, et les libellés des lignes sont sélectionnés.
-
Nous laissons par défaut la distance Euclidienne et la méthode de Ward en tant que méthode d’agrégation.
-
Dans l'onglet Options, les options Centrer et Réduire sont activées de manière à éviter que l'échelle des variables n'influe sur les résultats.
-
La troncature est activée et pour ne pas avoir à définir un nombre de classes arbitraire, nous utilisons l’indice de Hartigan. Cet indice permet de comparer la qualité de deux classifications en fonction de son évolution.
-
Nous voulons que le nombre de classes soit compris entre 2 et 5. L’indice de Hartigan définira donc automatiquement un nombre de classes compris dans cet intervalle.
-
Les calculs commencent lorsque vous cliquez sur le bouton OK.
Interpréter les résultats d'une Classification Ascendante Hiérarchique
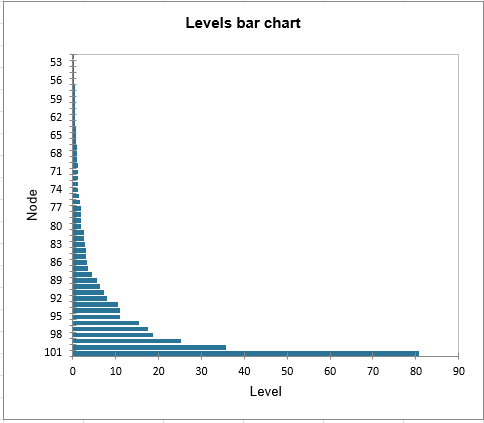
Les premiers résultats sont le tableau récapitulant les différentes étapes de l'algorithme, et le diagramme des niveaux des nœuds. Sa forme communique des informations sur la structure des données. Lorsque des sauts importants sont observés, nous avons une agrégation de structures hétérogènes.
Le graphique ci-dessous est le dendrogramme. Il représente de manière claire la façon dont l'algorithme procède pour regrouper les individus puis les sous-groupes. Finalement, l'algorithme a progressivement regroupé tous les individus.
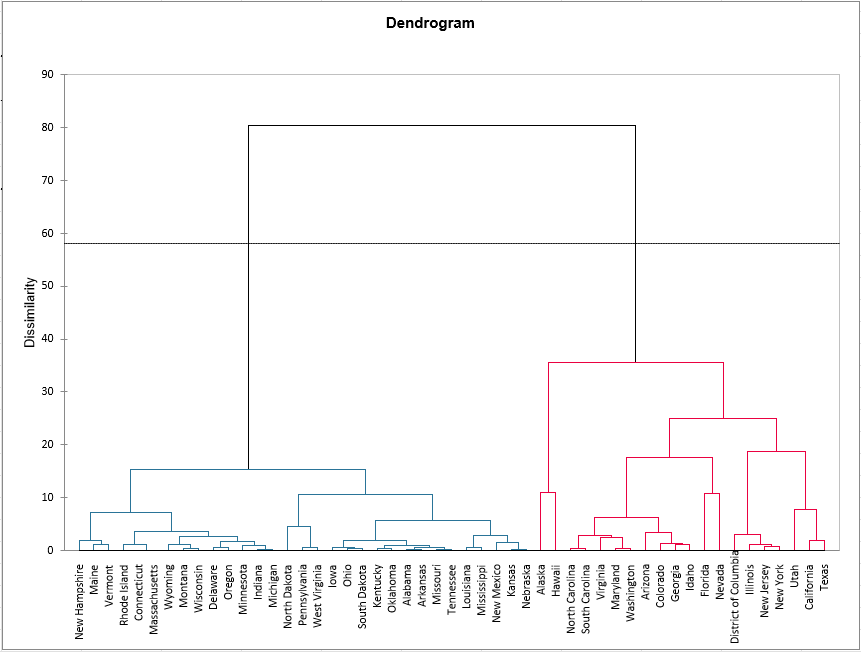
La ligne en pointillés représente la troncature et permet de visualiser que deux groupes ont été identifiés. Le premier groupe est plus homogène que le second groupe, en effet la hauteur du premier groupe (coloré en bleu) est plus faible que le second (coloré en rouge). L’indice de Hartigan a donc défini le nombre 2 comme étant le nombre de classes le plus approprié pour ces données. Il faut tenir compte du tableau suivant pour comprendre ce choix.
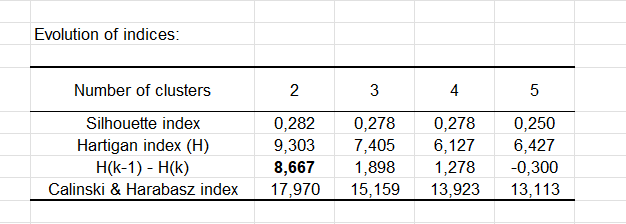
Le tableau nous informe sur l’évolution des indices de Silhouette, de Hartigan et de Calinski et Harabasz, pour chaque nombre de classes compris entre 2 et 5.
Dans notre cas, ce sont les lignes « Indice de Hartigan (H) » et « H(k-1) – H(k) » qui nous intéressent. Nous voyons l’évolution de l’indice de Hartigan sur la deuxième ligne, tandis que sur la troisième ligne, nous observons l’évolution de la différence entre deux indices obtenus avec une partition en k classes et une partition en (k-1) classes. C’est la plus grande différence (en gras dans le tableau) qui nous permet de choisir le nombre de classes approprié, à savoir 2 classes.
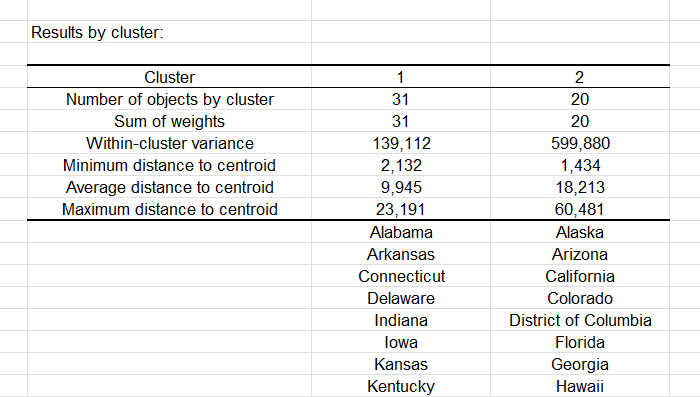
Grâce au tableau suivant, nous pouvons voir la répartition de chaque Etat dans les 2 classes. Nous pouvons voir aussi que la variance intra-classe de la classe 1 (à gauche sur le dendrogramme) est plus faible que la classe 2 (à droite), ce qui confirme une plus grande homogénéité de la classe 1.
Un tableau présente ensuite pour chaque Etat, l'identifiant de la classe à laquelle il a été affecté. Une partie du tableau est présentée ci-dessous. On pourra ensuite fusionner ces données avec le tableau initial pour d'éventuelles analyses complémentaires (une ANOVA par exemple pour connaître les variables qui contribuent le plus à la séparation des classes).
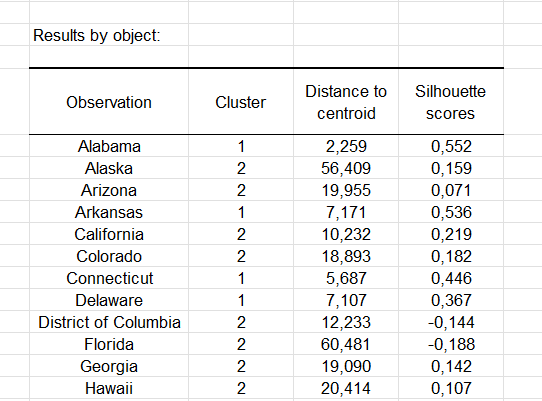
L’indice de Silhouette de chaque observation peut être aussi affiché, s’il est proche de 1 l’observation est alors jugée bien classée.
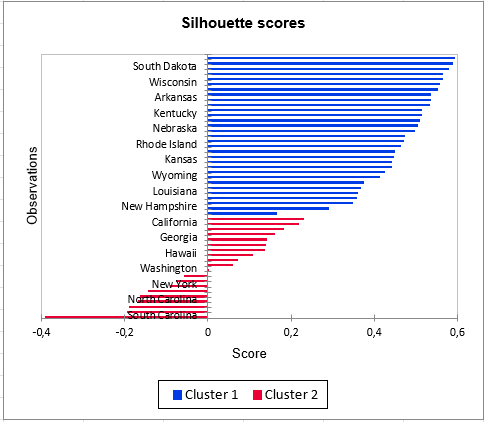
Ce dernier indice peut également être représenté sous forme de graphique, avec les observations triées dans l’ordre décroissant et par classe afin de juger la qualité de la classification obtenue. Des indices négatifs pour des observations de la classe 2 prouvent encore la faible homogénéité de cette classe en comparaison avec la classe 1.
Conclusion sur la classification avec la méthode de la Classification Ascendante Hiérarchique
La classification ascendante hiérarchique avec l’utilisation de l’indice de Hartigan a permis de séparer les États en deux groupes. Cependant un groupe est plus homogène que l’autre. Il est possible d’éviter cela en consolidant la classification grâce à l’algorithme de k-means. Pour cela, il vous suffit d’activer l’option de consolidation dans l’onglet Options.
Note : si vous utilisez une distance différente que la distance euclidienne ou un critère différent de celui de Ward, des adaptations des indices de Hartigan et de Calinski et Harabasz proposées par nos équipes vous permettront de vous guider quand même vers le meilleur choix du nombre de classes possible.
La vidéo ci-dessous vous montre comment réaliser ce tutoriel.
Cet article vous a t-il été utile ?
- Oui
- Non
