Analyse des pénalités, tutoriel dans Excel
Ce tutoriel vous aide à configurer et à interpréter une analyse de pénalité avec Excel en utilisant XLSTAT.
Jeu de données pour l'analyse des pénalités
Deux types de données sont utilisés dans cet exemple :
-
Les données de préférence (ou scores d'appréciation) qui correspondent à un sondage où une marque/type de chips a été évaluée par 150 consommateurs. Chaque consommateur a donné une note sur une échelle de 1 à 5 pour quatre attributs (Salé, Sucré, Acidité, Croquant) - 1 signifie "peu", et 5 "beaucoup" -, puis a donné un score global d'appréciation sur une échelle de Likert de 1 à 10.
-
Les données ont été collectées sur une échelle JAR (Just About Right) de 5 points. Elles correspondent à des évaluations allant de 1 à 5 pour quatre attributs (Salé, Sucré, Acidité, Croquant). 1 correspond à « Pas du tout assez », 2 à « Pas assez », 3 à « JAR » (Juste ce qu'il faut), un idéal pour le consommateur, 4 à « Trop » et 5 à « Beaucoup trop ».
But de ce tutoriel
Notre objectif est d'identifier quelques pistes possibles pour le développement d'un nouveau produit.
Paramétrer une analyse des pénalités
-
Une fois XLSTAT ouvert, cliquez sur Sensoriel / Tâches rapides / Analyse de pénalité.
-
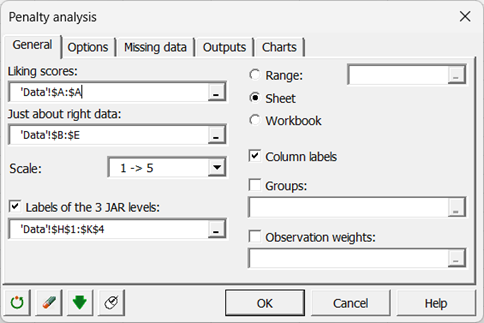
La boîte de dialogue Analyse de pénalité apparaît.
-
Nous sélectionnons les scores d'appréciation, puis les données JAR. Les étiquettes JAR à 3 niveaux sont également sélectionnées, car elles facilitent l'interprétation des résultats.
-
Dans l'onglet Options, nous définissons le seuil de la taille de l'échantillon en dessous duquel les tests de comparaison ne seront pas effectués, car ils pourraient ne pas être suffisamment fiables.
-
Dans les Sorties, la corrélation de Spearman a été choisie car les données sont ordinales.
-
Les calculs commencent une fois que vous avez cliqué sur OK. Les résultats seront ensuite affichés.
Interpréter les résultats d'une analyse des pénalités
Après les statistiques descriptives concernant les différentes variables de préférence et JAR, XLSTAT affiche la matrice des corrélations.
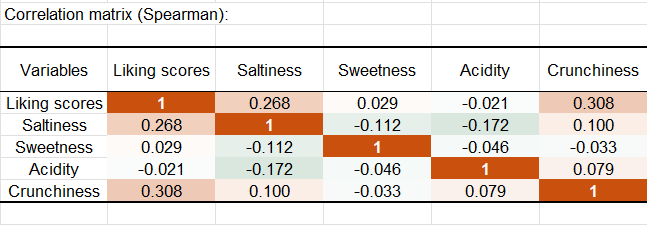
Les corrélations entre les données de préférence et les variables JAR ne devraient pas être interprétées car les données JAR ne sont pas de véritables données ordinales (5 est moins bien de 3 sur l'échelle JAR, alors que 5 est mieux que 3 sur l'échelle des préférences). Cependant si une corrélation entre une variable JAR et une variable de préférence est significativement différente de 0, cela peut signifier que la variable JAR a un faible impact sur la préférence : si elle avait un impact fort, la corrélation devrait idéalement être 0. Si le niveau « trop » a un impact moindre que le niveau « pas assez », la corrélation pourrait être positive, et vice-versa pour une corrélation négative.
Le tableau suivant est un résumé des données JAR. Le diagramme qui suit est basé sur ce tableau et permet de visualiser rapidement comment les données sont distribuées pour chaque dimension JAR.
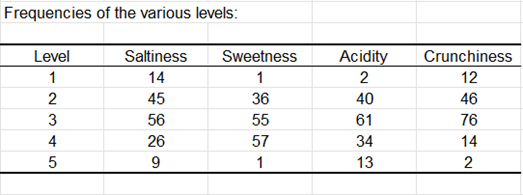
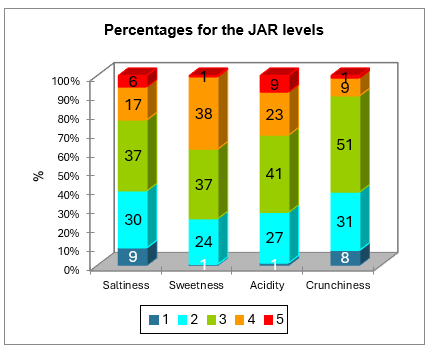
Les données sont ensuite agrégées sur une échelle à 3 niveaux. Le tableau et le diagramme correspondants sont affichés ci-dessous.
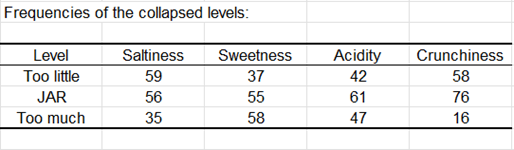
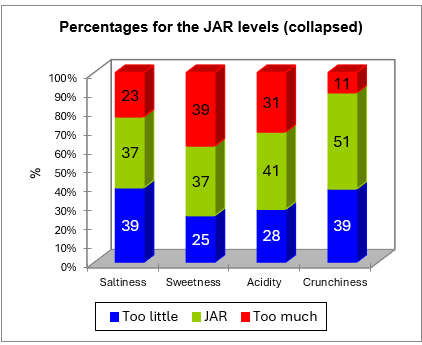
Le tableau ci-dessous correspond à l'analyse des pénalités.
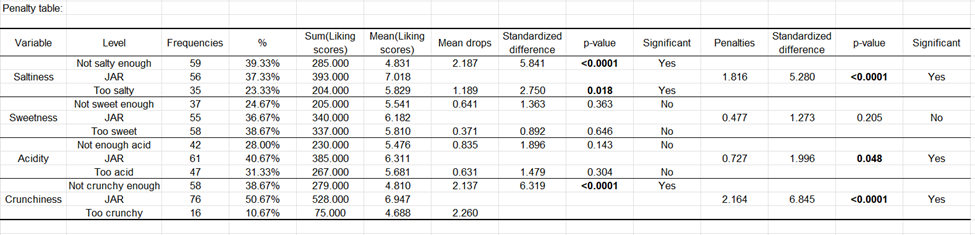
L'information suivante est montrée pour chaque dimension JAR :
-
Le nom de la dimension JAR.
-
Les 3 niveaux agrégés des données JAR.
-
Les fréquences correspondant à chaque niveau.
-
Les % correspondant à chaque niveau.
-
La somme des préférences correspondant à chaque niveau.
-
La préférence moyenne pour chaque niveau.
-
L'effet sur la moyenne pour les niveaux « trop » et « pas assez » (c'est la différence entre la préférence moyenne pour le niveau JAR et la moyenne calculée pour le niveau « trop » ou le niveau « pas assez ». Cette information est intéressante car elle montre combien de points de préférence sont perdus lorsque le produit est jugé « trop » ou « pas assez » par un consommateur.
-
Les différences standardisées sont des statistiques intermédiaires qui sont ensuite utilisées pour les tests de comparaison.
-
Les p-values correspondent au test de comparaison entre la moyenne du niveau JAR et les moyennes pour les deux autres niveaux (c'est une comparaison multiple avec 3 groupes).
-
Une interprétation est automatiquement fournie. Elle dépend du niveau de signification choisi (ici 5%).
-
La pénalité est ensuite calculée. C'est une différence pondérée entre les moyennes (préférence moyenne pour JAR - préférence moyenne pour les deux autres niveaux confondus). Cette statistique a donné son nom à la méthode. Elle montre combien de points de préférence sont perdus lorsque le produit ne correspond pas à l'attente du consommateur.
-
La différence standardisée est une statistique intermédiaire qui est ensuite utilisée pour le test de comparaison.
-
La p-value correspond au test de comparaison entre la moyenne pour le niveau JAR et la moyenne correspondant aux autres niveaux. Ce test revient à tester si la pénalité est sensiblement différente de 0 ou pas.
-
Une interprétation du test est automatiquement fournie, et dépend du niveau de signification choisi (ici 5%).
Pour la dimension salée, on constate que les clients pénalisent fortement le produit lorsqu'ils le jugent pas assez salé. Les deux effets sur la moyenne sont sensiblement différents de 0, tout comme la pénalité globale.
Pour la dimension sucrée, aucun des tests n'est significatif.
Pour la dimension de l'acidité, la pénalité globale est légèrement significative, bien que les deux effets sur la moyenne ne le soient pas. Cela signifie que l'acidité est importante pour les clients, mais cette enquête n'a peut-être pas été suffisamment puissante pour détecter quel effet spécifique sur la moyenne (pas assez d'acide et/ou trop acide) est concerné.
Pour le croustillant, l'effet sur la moyenne n'a pas pu être calculé pour le niveau "trop croustillant" car le % de cas dans ce niveau est inférieur au seuil de 20 % fixé précédemment. Lorsque le produit n'est pas assez croustillant, le produit est fortement pénalisé.
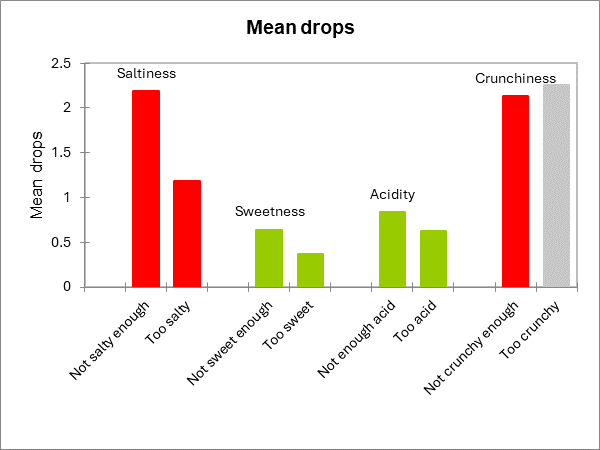
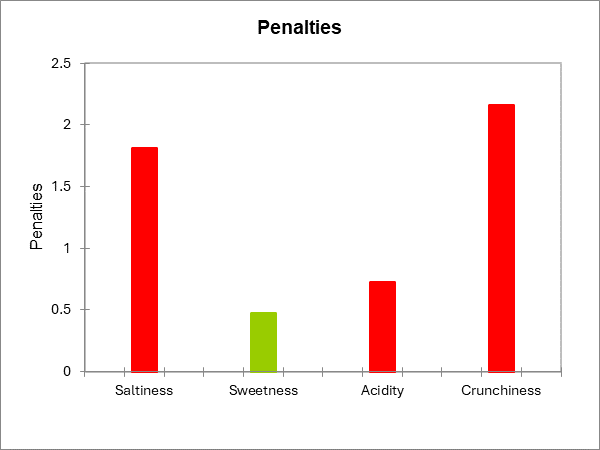
Les deux graphiques suivants résument les résultats décrits ci-dessus. Lorsqu'une barre est rouge, cela signifie que la différence est significative, lorsqu'elle est verte, la différence n'est pas significative, et lorsqu'elle est grise, le test n'a pas été calculé parce qu'il n'y avait pas assez de cas.
Cet article vous a t-il été utile ?
- Oui
- Non